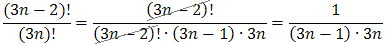Zadania z silni

Oblicz:

4! - 2! ⋅ 3! = 4! - 2! ⋅ 3! = 24 - 2 ⋅ 6 = 24 - 12 = 12
5! - 2! ⋅ 4! = 5! - 2! ⋅ 4! = 120 - 2 ⋅ 24 = 120 - 48 = 72
\(\frac{10!}{8!\cdot 2!}\)
W tym przykładzie występują już trochę większe liczby, zatem nie opłaca się liczyć ile dokładnie wynosi np. 10!. Łatwiej będzie skrócić wspólne czynniki z licznika i mianownika.
Zauważmy najpierw, że:

Zatem:
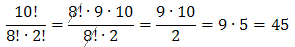
\(\frac{12!}{10!\cdot 4!}\)
W tym przykładzie skrócimy wspólne czynniki z licznika oraz mianownika.
Zauważmy najpierw, że:

Zatem:
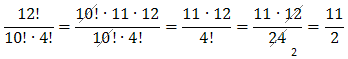
\(\frac{9!\cdot 7!}{(6!)^3}\)
Podobnie jak w przykładach poprzednich - skrócimy wspólne czynniki z licznika i mianownika.
Zauważmy najpierw, że:

Zatem podstawiamy i skracamy:
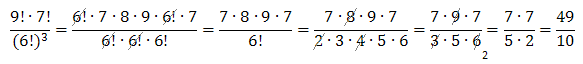
\(\frac{(9!)^3}{10!\cdot (8!)^2}\)
W tym przykładzie również skrócimy wspólne czynniki z licznika i mianownika. Wcześniej będziemy musieli jednak "sprowadzić" wszystkie silnie do najmniejszej, czyli do 8!.
Zauważmy, że:

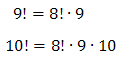
W związku z tym podstawiamy i skracamy:

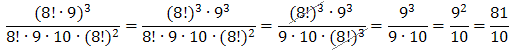
Doprowadź do najprostszej postaci:

\(\frac{n!}{(n-1)!}\)
W tym zadaniu (podobnie jak w zadaniu poprzednim) skrócimy wspólne czynniki z licznika i mianownika. Na początku będziemy musieli jednak tak zapisać wyrażenie n!, aby pojawił się wspólny czynnik na górze i na dole ułamka.
Zauważmy najpierw, że w n! siedzi ukryta (n-1)!:

Zatem podstawiamy i skracamy:
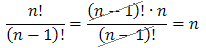
\(\frac{n!}{(n-3)!}\)
Liczba n! występująca w liczniku ułamka jest większa od liczby (n - 3)! występującej w mianowniku ułamka. Chcąc uzyskać wspólny czynnik w liczniku i mianowniku (aby go potem skrócić) przedstawimy większą z tych liczb jako mniejsza razy coś. Liczbę n! możemy zapisać np. tak:

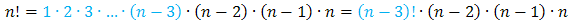
Teraz możemy już podstawić i skrócić ułamek:
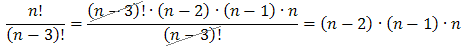
\(\frac{(n-2)!}{n!}\)
Tutaj postępujemy dokładnie tak samo jak w poprzednim przykładzie. Na początku zauważamy, że:

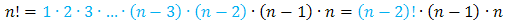
Zatem:
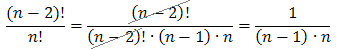
\(\frac{(n-3)!}{(n-1)!}\)
Zauważmy, że wyrażenie z mianownika możemy zapisać tak:

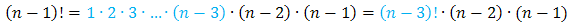
Dzięki takiemu przekształceniu uzyskamy wspólny czynnik w liczniku oraz w mianowniku ułamka i będziemy mogli go skrócić:

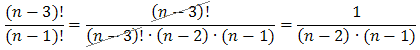
Tego typu "sztuczkę" bardzo często wykorzystuje się przy skracaniu ułamków z silnią. Wystarczy jedynie zapamiętać, że zawsze w większej liczbie szukamy wspólnego czynnika dla mniejszej.
\(\frac{(2n)!}{(2n-3)!}\)
Liczba w liczniku jest większa, więc zapiszemy ją tak aby pojawił się czynnik z mianownika:

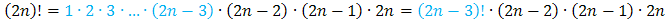
Dzięki takiemu zapisaniu uzyskamy wspólny czynnik w liczniku i w mianowniku ułamka. Teraz będziemy mogli go skrócić:
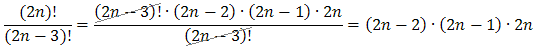
\(\frac{(3n-2)!}{(3n)!}\)
Liczba w mianowniku jest większa, więc zapiszemy ją tak aby pojawił się czynnik z licznika:

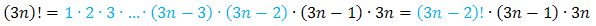
Dzięki takiemu zapisaniu mianownika uzyskamy wspólny czynnik w liczniku i w mianowniku ułamka. Teraz będziemy mogli go skrócić: