Wzór de Moivre'a - potęgowanie liczb zespolonych
Poziom studiów
Liczby zespolone \(z, w \in \mathbb{C}\), z argumentami odpowiednio: \(\alpha \) i \(\beta \), Możemy zapisać w postaci trygonometrycznej: 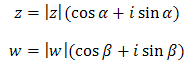 Obliczymy teraz iloczyn tych liczb zapisanych w postaci trygonometrycznej:
Obliczymy teraz iloczyn tych liczb zapisanych w postaci trygonometrycznej: 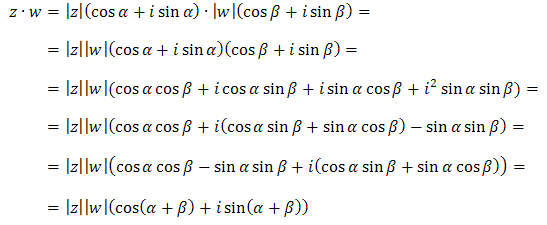 Ostatnia równość wynika ze wzorów trygonometrycznych na cosinus sumy kątów oraz na sinus sumy kątów.
Ostatnia równość wynika ze wzorów trygonometrycznych na cosinus sumy kątów oraz na sinus sumy kątów.Powyższy rachunek pokazuje, że przy mnożeniu dwóch liczb zespolonych \(z, w \in \mathbb{C}\) otrzymujemy liczbę zespoloną, której:
- moduł jest iloczynem modułów liczb \(z\) oraz \(w\),
- argument jest sumą argumentów liczb \(z\) oraz \(w\).
Wzór de Moivre'a
Dla dowolnej liczby \(z\in \mathbb{C} \) zachodzi następujący wzór: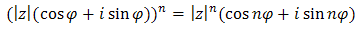
Przy pomocy tego wzoru można szybko podnosić liczby zespolone do dowolnie dużych potęg.
Dana jest liczba \(z=1-i\). Oblicz \(z^{100}\).
Zacznijmy od zapisania liczby zespolonej \(z=1-i\) w postaci trygonometrycznej.
Zaznaczmy ją w układzie współrzędnych:
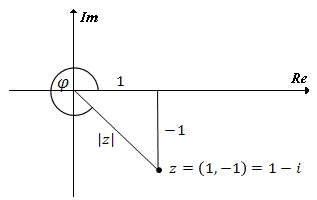 Obliczamy moduł: \[|z|=\sqrt{1^2+(-1)^2}=\sqrt{2}\] Obliczamy argument:
Obliczamy moduł: \[|z|=\sqrt{1^2+(-1)^2}=\sqrt{2}\] Obliczamy argument: 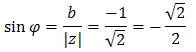 Kąt \(\varphi\) leży w IV ćwiartce układu współrzędnych, zatem:
Kąt \(\varphi\) leży w IV ćwiartce układu współrzędnych, zatem: 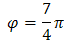
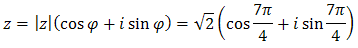 Korzystając ze wzoru de Moivre'a liczymy, że:
Korzystając ze wzoru de Moivre'a liczymy, że: 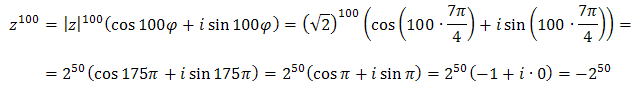
Zaznaczmy ją w układzie współrzędnych:
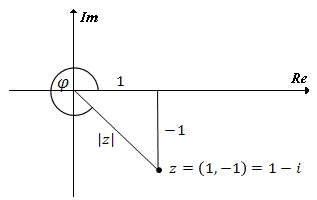 Obliczamy moduł: \[|z|=\sqrt{1^2+(-1)^2}=\sqrt{2}\] Obliczamy argument:
Obliczamy moduł: \[|z|=\sqrt{1^2+(-1)^2}=\sqrt{2}\] Obliczamy argument: 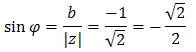 Kąt \(\varphi\) leży w IV ćwiartce układu współrzędnych, zatem:
Kąt \(\varphi\) leży w IV ćwiartce układu współrzędnych, zatem: 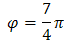
Argument można było również odczytać z układu współrzędnych. Widać, że \(\varphi = 3 \cdot 90^\circ + 45^\circ = 315^\circ\).
Zapiszmy teraz liczbę \(z=1-i\) w postaci trygonometrycznej: 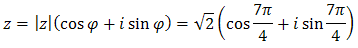 Korzystając ze wzoru de Moivre'a liczymy, że:
Korzystając ze wzoru de Moivre'a liczymy, że: 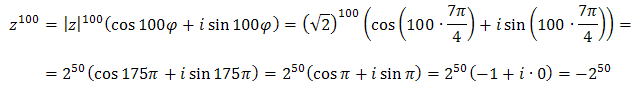
Dana jest liczba \(z = -1+\sqrt{3}i\). Oblicz \(z^{67}\).
Zaznaczamy liczbę \(z = -1+\sqrt{3}i\) w układzie współrzędnych: 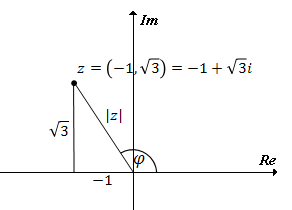 Teraz obliczamy moduł: \[|z|=\sqrt{(-1)^2+(\sqrt{3})^2}=\sqrt{4}=2\] Obliczamy argument:
Teraz obliczamy moduł: \[|z|=\sqrt{(-1)^2+(\sqrt{3})^2}=\sqrt{4}=2\] Obliczamy argument: 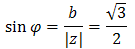 Kąt \(\varphi\) leży w II ćwiartce układu współrzędnych, zatem:
Kąt \(\varphi\) leży w II ćwiartce układu współrzędnych, zatem: 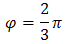
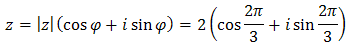 Stosując wzór de Moivre'a obliczamy, że:
Stosując wzór de Moivre'a obliczamy, że: 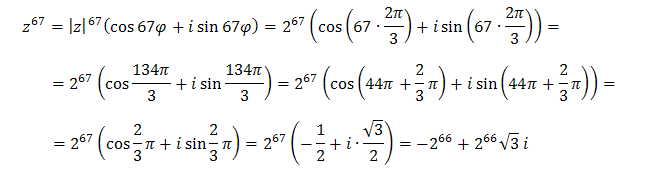
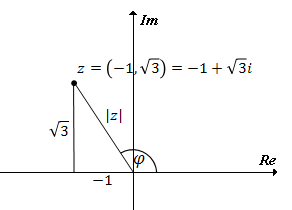 Teraz obliczamy moduł: \[|z|=\sqrt{(-1)^2+(\sqrt{3})^2}=\sqrt{4}=2\] Obliczamy argument:
Teraz obliczamy moduł: \[|z|=\sqrt{(-1)^2+(\sqrt{3})^2}=\sqrt{4}=2\] Obliczamy argument: 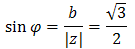 Kąt \(\varphi\) leży w II ćwiartce układu współrzędnych, zatem:
Kąt \(\varphi\) leży w II ćwiartce układu współrzędnych, zatem: 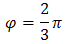
Argument można było również odczytać z układu współrzędnych. Widać, że \(\varphi = 90^\circ + 30^\circ = 120^\circ\).
Zapiszmy teraz liczbę \(z = -1+\sqrt{3}i\) w postaci trygonometrycznej: 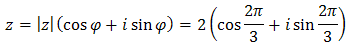 Stosując wzór de Moivre'a obliczamy, że:
Stosując wzór de Moivre'a obliczamy, że: 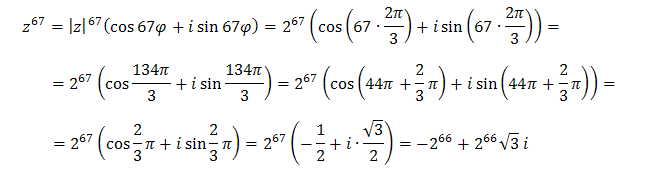
Tematy nadrzędne i sąsiednie