Wartości funkcji i odczytywanie ich z wykresu

Poziom podstawowy

Przypomnienie

Z wykresu funkcji w układzie współrzędnych można odczytać:

argumenty z poziomej osi \(x\)-ów,
wartości z pionowej osi \(y\)-ów.

Ze wzoru funkcji można obliczyć wartość, jaką przyjmuje funkcja dla dowolnego argumentu \(x\).
Wystarczy podstawić we wzorze funkcji pod \(x\)-a podaną liczbę, a w rezultacie otrzymamy szukaną wartość \(y\).

Oblicz jaką wartość przyjmuje funkcja \( y = 2x + 3 \) dla \( x = 5 \).

Do wzoru funkcji: \[y = 2\color{Red}x\color{black} + 3\] podstawiamy pod \(x\)-a liczbę \( 5 \): \[y = 2\cdot \color{Red}5\color{black} + 3\] i otrzymujemy: \[y = 2\cdot 5 + 3 = 10 + 3 = 13\] Zatem dla argumentu \(x = 5\) funkcja przyjmuje wartość \(y = 13\).

Oblicz jaką wartość przyjmuje funkcja \( y = x^2 - 5x + 1 \) dla \(x = -3\).

Do wzoru funkcji: \[ y = x^2 - 5{x} + 1 \] podstawiamy pod \(x\)-a liczbę \(-3\): \[ y = (-3)^2 - 5\cdot (-3) + 1 \] otrzymując, że: \[ y = 9 + 15 + 1 = 25 \] Zatem dla argumentu \(x = -3\) funkcja przyjmuje wartość \(y = 25\).

Do odczytywania wartości funkcji z wykresu niezbędna jest umiejętność zaznaczania i odczytywania współrzędnych punktów w układzie współrzędnych.

Dany jest wykres funkcji:

Odczytaj wartości jakie przyjmuje ta funkcja dla argumentów \(x=-6\), \(x=-4\), \(x=2{,}5\) oraz \(x=6\).

Zaznaczamy na wykresie punkty dla podanych argumentów \(x\).

Odczytujemy z wykresu, że:

dla argumentu \(x=-6\) funkcja przyjmuje wartość \(y=4\),
dla argumentu \(x=-4\) funkcja przyjmuje wartość \(y=0\),
dla argumentu \(x=2{,}5\) funkcja przyjmuje wartość \(y=2\),
dla argumentu \(x=6\) funkcja przyjmuje wartość \(y=-1\).

Dany jest wykres funkcji:

Odczytaj z wykresu dla jakich argumentów \(x\) funkcja przyjmuje wartość:

\(y=6\)

\(y=2\)

\(y=0\)

\(y=-3\)

\(y=-5\)

Z wykresu:

odczytujemy, że:

wartość \(y=6\) funkcja przyjmuje dla \(x = -7\),

wartość \(y=2\) funkcja przyjmuje dla \(x = -5\) oraz dla \(x \in \langle -2, 4\rangle \),

wartość \(y=0\) funkcja przyjmuje dla \(x = -4\), \(x = -2{,}5\) oraz dla \(x = 5\),

wartość \(y=-3\) funkcja przyjmuje dla \(x = 8\),

wartości \(y=-5\) funkcja nie przyjmuje dla żadnego \(x\)-a.

W tym nagraniu wideo pokazuję jak odczytywać wartości funkcji z wykresu.

Na rysunku przedstawiony jest wykres funkcji \(f(x)\) określonej dla \(x\in [-7, 8]\).

Odczytaj z wykresu i zapisz:
a) największą wartość funkcji \(f\),
b) zbiór rozwiązań nierówności \(f(x)\lt 0\).

a) \(7\); b) \(x\in (-3;5)\)

Zbiorem wartości funkcji przedstawionej na rysunku jest przedział

A.\(\langle -3,6 \rangle\)

B.\(\langle -1,4 \rangle\)

C.\((1,3)\)

D.\((-2,2)\)

Zbiorem wartości funkcji, której wykres przedstawiono na rysunku jest przedział:

A.\( \langle -4,5 \rangle \)

B.\( \langle -3,4 \rangle \)

C.\( \langle -2,4 \rangle \)

D.\( \langle -3,2 \rangle \)

Na rysunku przedstawiony jest wykres funkcji \(y = f(x)\).

Zbiorem wartości tej funkcji jest

A.\( \langle -4,3 \rangle \)

B.\( \langle -4,-1 \rangle \cup \langle 1,3 \rangle\)

C.\( \langle -4,-1 \rangle \cup ( 1,3 \rangle \)

D.\( \langle -5,6 \rangle \)

Na rysunku przedstawiono wykres funkcji \(f\).

Odczytaj z wykresu i zapisz:

zbiór wartości funkcji \(f\),
przedział maksymalnej długości, w którym \(f\) jest malejąca.

a) \(\langle -2;3 \rangle \)
b) \(\langle -2;2 \rangle \)

Na rysunku przedstawiono wykres funkcji \(y=f(x)\).

Największa wartość funkcji \(f\) w przedziale \([-1,1]\) jest równa

A.\( 4 \)

B.\( 3 \)

C.\( 2 \)

D.\( 1 \)

Rysunek przedstawia wykres pewnej funkcji \( y=f(x) \), określonej dla \( x \in \langle -4,4 \rangle \).

Zbiór wszystkich argumentów, dla których funkcja \( f \) przyjmuje wartości niedodatnie, to zbiór

A.\(\langle 0,3 )\cup ( 3,4 \rangle \)

B.\(\langle -4,-3 \rangle\cup \langle 0,4 \rangle \)

C.\((-4,-3)\cup (0,3)\cup (3,4) \)

D.\((-2,1)\cup (3,4) \)

Zbiorem wartości funkcji \(f\) jest przedział

A.\( \langle -3,5 \rangle \)

B.\( \langle -6,7 \rangle \)

C.\( \langle 0,6 \rangle \)

D.\( \langle -5,8 \rangle \)

Przedziałem, w którym funkcja \(f\) przyjmuje tylko wartości ujemne, jest

A.\( \langle 5,0 \rangle \)

B.\( ( 5,7 \rangle \)

C.\( \langle 0,7 \rangle \)

D.\( \langle -6,5 \rangle \)

Na rysunku przedstawiono wykres funkcji \(f\).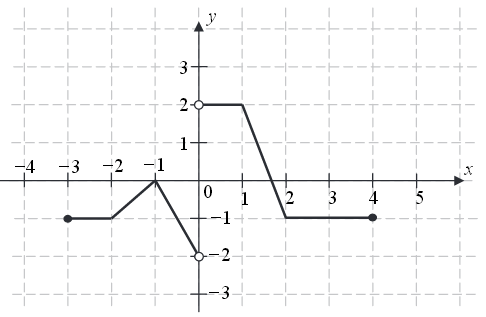

Zbiorem wartości funkcji \(f\) jest

A.\( (-2,2\rangle \)

B.\( \langle -2,2\rangle \)

C.\( \langle -2,2) \)

D.\( (-2,2) \)

Funkcja \(f\) jest określona wzorem \(f(x)=\frac{2x}{x-1}\) dla \(x\ne 1\). Wartość funkcji \(f\) dla argumentu \(x=2\) jest równa

A.\( 2 \)

B.\( -4 \)

C.\( 4 \)

D.\( -2 \)

Do wykresu funkcji \( f(x)=\frac{a}{x+1} \) określonej dla \(x\ne -1\) należy punkt \( A=(-2,3) \) dla \( a \) równego:

A.\(-3 \)

B.\(3 \)

C.\(-8 \)

D.\(8 \)

Do wykresu funkcji \(f(x)=\frac{a}{x-3}\) należy punkt \(A=(1,2)\). Wobec tego:

A.\( a=-4 \)

B.\( a=-3 \)

C.\( a=-2 \)

D.\( a=-1 \)

Punkt \(P=(a+1,2)\) należy do wykresu funkcji \(f(x)=\frac{4}{x}\). Liczba \(a\) jest równa

A.\( 0 \)

B.\( -1 \)

C.\( 2 \)

D.\( 1 \)

Funkcja \(f\) jest określona wzorem \(f(x)=\frac{2x-b}{x-9}\) dla \(x \ne 9\). Ponadto wiemy, że \(f(4)=-1\). Oblicz współczynnik \(b\).

\(b=3\)

Dana jest funkcja \(f(x)=\frac{x^2+2}{1-b}\). Oblicz współczynnik \(b\) jeżeli wiadomo, że \(f(2) = -3\).

\(b=3\)

Funkcja \(f\) określona jest wzorem \(f(x)=\sqrt{x+2\sqrt{6}}\). Wartość funkcji \(f\) dla argumentu \(x=(\sqrt{3}-\sqrt{2})^2\) jest równa

A.\( \sqrt{2} \)

B.\( \sqrt{3} \)

C.\( \sqrt{5} \)

D.\( \sqrt{6} \)

Funkcja \(f\) jest określona wzorem \(f(x)=\frac{2x-8}{x}\) dla każdej liczby rzeczywistej \(x \ne 0\). Wówczas wartość funkcji \(f(\sqrt{2})\) jest równa

A.\( 2-4\sqrt{2} \)

B.\( 1-2\sqrt{2} \)

C.\( 1+2\sqrt{2} \)

D.\( 2+4\sqrt{2} \)

Dana jest funkcja \(f\) określona wzorem \(f(x)=\begin{cases} x-2\quad \text{dla } x\le 0 \\ \Bigl ||x+3|-4 \Bigl |\quad \text{dla } x\gt 0 \end{cases} \). Równanie \(f(x)=1\) ma dokładnie

A.jedno rozwiązanie

B.dwa rozwiązania

C.cztery rozwiązania

D.pięć rozwiązań

Znajdź wszystkie argumenty \(x\) dla których funkcje \(f(x)=x-3\) oraz \(g(x)=-\frac{2}{x}\) przyjmują tę samą wartość.

\(x=1\) lub \(x=2\)