Potęgowanie - wprowadzenie
Szkoła podstawowa
Potęgi zapisujemy tak: 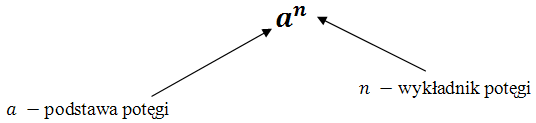
Definicja
Potęga liczby \(a\) o wykładniku naturalnym \(n\), to: \[a^n=\underbrace{a\cdot a\cdot a\cdot...\cdot a}_{n \text{ razy}}\] Oto przykłady stosowania definicji i zamieniania potęg na iloczyny:
- \(5^3 = 5 \cdot 5 \cdot 5\)
- \(5^7 = 5 \cdot 5 \cdot 5 \cdot 5 \cdot 5 \cdot 5 \cdot 5\)
- \(2^4 = 2 \cdot 2 \cdot 2 \cdot 2\)
- \(3^2 = 3 \cdot 3\)
- \(3^{10} = 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3\)
- \(3^{11} = 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3\)
- \(3^{12} = 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3\)
- \(x^3 = x \cdot x \cdot x\)
- \(x^4 = x \cdot x \cdot x \cdot x\)
- \((5x)^4 = (5x) \cdot (5x) \cdot (5x) \cdot (5x)\)
- \((5x)^6 = (5x) \cdot (5x) \cdot (5x) \cdot (5x) \cdot (5x) \cdot (5x)\)
- \((5x - 2)^2 = (5x - 2) \cdot (5x - 2) \)
Za pomocą potęg możemy w prosty sposób zapisywać długie iloczyny takich samych liczb (co widać na powyższych przykładach).
Na potęgach można wykonywać różne działania, które zostaną omówione w kolejnych rozdziałach.
Tematy nadrzędne i sąsiednie