Matura podstawowa - zadania CKE (2015-2023)
Poziom podstawowy
Poniżej znajduje się zestaw 134 zadań treningowych przygotowany przez CKE.Na początku roku akademickiego mężczyźni stanowili \(40\%\) wszystkich studentów. Na koniec roku liczba wszystkich studentów zmalała o \(10\%\) i wówczas okazało się, że mężczyźni stanowią \(33\frac{1}{3}\%\) wszystkich studentów. O ile procent zmieniła się liczba mężczyzn na koniec roku w stosunku do liczby mężczyzn na początku roku?
Funkcja \(f\) jest funkcją kwadratową. Zbiorem wszystkich rozwiązań nierówności \(f(x)\lt 0\) jest przedział \((1,5)\). Rozwiąż nierówność \(-f(x+3)\lt 0\).
Wartość wyrażenia \(\frac{\sqrt[3]{4}\cdot \sqrt[3]{-16}}{-8}\) jest równa
A.\( 2^{\frac{1}{3}} \)
B.\( 2^{\frac{1}{2}} \)
C.\( 2^{-1} \)
D.\( 2^{-2} \)
Odwrotnością liczby \(2\sqrt{2}\cdot \left(\frac{1}{8}\right)^{-\frac{4}{3}}\) jest liczba
A.\( -2^{\frac{11}{2}} \)
B.\( -2^{-\frac{11}{2}} \)
C.\( 2^{-\frac{11}{2}} \)
D.\( 2^{\frac{11}{2}} \)
Liczba \(\sqrt[3]{4^{-1}}\cdot 2^{\frac{1}{4}}\cdot 16^{\frac{1}{3}}\) jest równa
A.\( 2^{\frac{1}{6}} \)
B.\( 2^{\frac{1}{4}} \)
C.\( 2^{\frac{1}{3}} \)
D.\( 2^{\frac{11}{12}} \)
Dane są liczby \(a=\log 3\), \(b=\log 2\). Wyznacz logarytm dziesiętny z liczby \(72\) za pomocą \(a\) i \(b\).
Liczba o \(2\) większa od liczby \(\log_5 4\) jest równa
A.\( \log_5 6 \)
B.\( \log_5 8 \)
C.\( \log_5 29 \)
D.\( \log_5 100 \)
Na lokacie złożono \(1000\) zł przy rocznej stopie procentowej \(p\%\) (procent składany). Odsetki naliczane są co kwartał. Po upływie roku wielkość kapitału na lokacie będzie równa
A.\( 1000\left( 1+\frac{4p}{100} \right) \)
B.\( 1000\left( 1+\frac{p}{100} \right)^4 \)
C.\( 1000\left( 1+\frac{p}{400} \right) \)
D.\( 1000\left( 1+\frac{p}{400} \right)^4 \)
Dany jest trójkąt o bokach długości \(a\), \(b\), \(c\). Stosunek \(a:b:c\) jest równy \(3:5:7\). Które zdanie jest fałszywe?
A.Liczba \(c\) jest o \(12{,}5\%\) mniejsza od liczby \(a+b\).
B.Liczba \(a\) stanowi \(20\%\) liczby \(a+b+c\).
C.Liczba \(a\) stanowi \(25\%\) liczby \(b+c\).
D.Liczba \(b\) to \(60\%\) liczby \(c\).
Nominalna stopa oprocentowania lokaty wynosi \(3\%\) w stosunku rocznym (bez uwzględnienia podatku). Odsetki kapitalizowane są na koniec każdego kolejnego okresu czteromiesięcznego. Oblicz, jaką kwotę wpłacono na tę lokatę, jeśli na koniec ośmiu miesięcy oszczędzania na rachunku lokaty było o \(916{,}56\) zł więcej niż przy jej otwarciu.
W pewnej szkole przez trzy kolejne lata zmieniała się liczba uczniów. W pierwszym roku liczba uczniów zmalała i na koniec roku była o \(10\%\) mniejsza niż na początku. W drugim roku wzrosła i ukończyło go \(20\%\) więcej uczniów niż pierwszy. O ile procent, w stosunku do liczby uczniów kończących drugi rok, zmniejszyła się ich liczba w następnym roku, jeśli na koniec trzeciego roku było tyle samo uczniów co na początku pierwszego? Wynik zaokrąglij do \(0{,}1\%\).
Autobus nazywamy przepełnionym, jeżeli w pewnym momencie znajduje się w nim co najmniej \(50\) pasażerów. Dwóch inspektorów monitoruje liczbę pasażerów w tych samych dziesięciu autobusach. Jeden z nich obliczył, jaki procent wszystkich autobusów stanowią autobusy przepełnione, a drugi - jaki procent wszystkich pasażerów w \(10\) autobusach stanowili pasażerowie podróżujący przepełnionymi pojazdami. Wiadomo, że liczba autobusów przepełnionych należy do zbioru \(\{1,2,...,9\}\). Który z inspektorów otrzymał większą liczbę?
Dane są liczby: \[\begin{split} &a=3\log_3 2-\log_3 16\\[6pt] &b=2\log_3 6-\log_3 18 \end{split}\] Wykaż, że \(a+b=0\).
Uzasadnij, że dla wszystkich liczb rzeczywistych dodatnich \(x\) różnych od \(\frac{1}{3}\) wartość wyrażenia \[\log_{3x}\bigl(3x^2\bigl)+\log_{3x}\bigl(9x\bigl)\] jest większa od \(2\).
Na rysunku przedstawiono wykresy trzech parami przecinających się prostych.  Te proste to:
Te proste to:
 Te proste to:
Te proste to: A.\(\begin{split}&x-2y=-1\\&3x+y=11\\&3x+8y=-17\end{split}\)
B.\( \begin{split}&x-2y=-1\\&3x+y=-11\\&3x+8y=-17\end{split} \)
C.\( \begin{split}&x-2y=1\\&3x+y=11\\&3x+8y=-17\end{split} \)
D.\( \begin{split}&x-2y=-1\\&3x+y=11\\&3x+8y=17\end{split} \)
Dany jest trójkąt \(ABC\), którego boki zawierają się w prostych o równaniach: \(y=\frac{1}{2}x+1\), \(y=7-x\) oraz \(y=0\). Oblicz pole trójkąta \(ABC\).
Wyznacz takie liczby \(a\) i \(b\), dla których układ równań \(\begin{cases} 4x+y+2=0\\ax^2+y+b=0 \end{cases} \) jest sprzeczny, zaś układ równań \(\begin{cases} 4x+y-2=0\\b^2x+y+a=0 \end{cases}\) ma nieskończenie wiele rozwiązań.
Rozwiązaniem układu równań pierwszego stopnia z dwiema niewiadomymi jest para różnych dodatnich liczb całkowitych. Jednym z równań tego układu jest \(2x+y=6\). Wyznacz drugie równanie układu, wiedząc, że jest to równanie prostej przechodzącej przez początek układu współrzędnych.
Wśród podanych poniżej nierówności wskaż tę, której zbiorem rozwiązań jest przedział \((-3,1)\).
A.\( x(x+2)\lt 3 \)
B.\( x(x+4)\lt 1 \)
C.\( x(x+3)\lt 1 \)
D.\( x(x+1)\lt 3 \)
W tabelce podano wartości funkcji kwadratowej \(f(x)=ax^2+bx+c\) dla wybranych trzech argumentów.
Rozwiąż nierówność \(f(x)\ge 0\).
| \(x\) | \(0\) | \(1\) | \(6\) |
| \(f(x)\) | \(-2\frac{1}{2}\) | \(0\) | \(-2\frac{1}{2}\) |
Rozważmy prostokąt o polu mniejszym od \(24\), w którym jeden bok jest od drugiego dłuższy o \(5\). Oblicz długość dłuższego boku prostokąta, jeśli jest ona liczbą całkowitą parzystą.
Równanie \(\frac{3(2-x)}{4x-3}=\frac{3}{2}\) nie ma takiego samego rozwiązania, jak równanie:
A.\( 6(2-x)=3(4x-3) \)
B.\( \frac{2}{3}(6-3x)=4x-3 \)
C.\( 9(2-x)=2(4x-3) \)
D.\( 3(2-x)=\frac{3}{2}(4x-3) \)
Do wyrażenia \(\frac{1}{x+1}\) określonego dla \(x\ne -1\) dodano jego odwrotność. Oblicz \(x\), dla którego otrzymana suma jest równa \(2\).
Do napełniania basenu służą dwie pompy. Pierwsza z nich ma wydajność o \(20\%\) większą niż druga. Napełnienie pustego basenu tylko drugą pompą trwa o \(1\) godzinę i \(40\) minut dłużej niż przy użyciu tylko pierwszej pompy. Oblicz, jaką część pustego basenu napełnią w ciągu jednej godziny obie pompy, pracując jednocześnie.
Na rysunku przedstawiony jest fragment wykresu funkcji kwadratowej \(f\).  Osią symetrii paraboli jest prosta o równaniu \(x=-3\). Rozwiązaniem nierówności \(f(x)\le 0\) jest zbiór
Osią symetrii paraboli jest prosta o równaniu \(x=-3\). Rozwiązaniem nierówności \(f(x)\le 0\) jest zbiór
 Osią symetrii paraboli jest prosta o równaniu \(x=-3\). Rozwiązaniem nierówności \(f(x)\le 0\) jest zbiór
Osią symetrii paraboli jest prosta o równaniu \(x=-3\). Rozwiązaniem nierówności \(f(x)\le 0\) jest zbiór A.\( \langle 0,-3\rangle \)
B.\( \langle -3,3\rangle \)
C.\( \langle -6,3\rangle \)
D.\( \langle -9,3\rangle \)
Funkcja \(W\) jest określona wzorem \(W(x)=3x^4-bx-2a\) dla wszystkich liczb rzeczywistych. Równość \(W(-1)+W(1)=0\) zachodzi, gdy
A.\( a=\frac{2}{3} \)
B.\( a=\frac{3}{2} \)
C.\( a=1 \)
D.\( a=-1 \)
Na tablicy zapisano następujące potęgi: \(\left(2^2\right)^{(2^2)}, \left(2\right)^{(2^{2^2})}, \left(2^{2^2}\right)^2, \left(2\right)^{{\left(2^2\right)}^2}\). Ile różnych liczb reprezentują te zapisy?
A.\( 4 \)
B.\( 3 \)
C.\( 2 \)
D.\( 1 \)
Wyznacz wzór funkcji kwadratowej \(f\) w postaci ogólnej, wiedząc, że zbiorem wartości tej funkcji jest przedział \((-\infty ,-1\rangle \), a wartość \(-5\) osiąga ona dla dwóch argumentów: \(2\) i \(10\).
Na rysunku są przedstawione fragmenty wykresów funkcji kwadratowych \(f\) i \(g\). Funkcja \(f\) jest określona wzorem \(f(x)=-x^2+6x-5\), a mniejsze z jej miejsc zerowych jest jednocześnie miejscem zerowym funkcji \(g\). Wierzchołek \(W\) paraboli, która jest wykresem funkcji \(f\), leży na wykresie funkcji \(g\), a wierzchołek \(Z\) paraboli będącej wykresem funkcji \(g\) leży na osi \(Oy\) układu współrzędnych. Wyznacz wzór funkcji \(g\). 

Różnica największej i najmniejszej wartości, jakie funkcja kwadratowa \[f(x)=-\frac{1}{2}x^2-2x+6\] przyjmuje w przedziale \(\langle -3,k\rangle \) dla \(k\gt 0\) jest równa \(4\frac{1}{2}\). Oblicz \(k\).
Na rysunku 1. jest przedstawiony wykres funkcji \(f\), a na rysunku 2. - wykres funkcji \(g\).  Funkcja \(g\) jest określona wzorem
Funkcja \(g\) jest określona wzorem
 Funkcja \(g\) jest określona wzorem
Funkcja \(g\) jest określona wzorem A.\( g(x)=-f(x) \)
B.\( g(x)=f(-x) \)
C.\( g(x)=f(x)+4 \)
D.\( g(x)=f(x)-4 \)
Wyznacz wartość największą funkcji \(f(x)=\frac{1}{x^2+4x-1}\) w przedziale \(\langle 1,3\rangle \).
Funkcja \(f\), której dziedziną jest zbiór \(\langle -1,5\rangle \), jest określona wzorem \(f(x)=-x^2+6x+5\). Wyznacz zbiór wszystkich wartości funkcji \(f\).
Wykres funkcji kwadratowej \(f\) przecina oś \(Ox\) w punktach \(x=1\) oraz \(x=3\) i przechodzi przez punkt \((0,-3)\). Wykres ten przesunięto i otrzymano wykres funkcji kwadratowej \(g(x)=f(x-p)\). Wierzchołek funkcji \(g\) leży na osi \(Oy\). Wyznacz wzór funkcji \(g\).
Parabola, która jest wykresem funkcji kwadratowej \(f(x)=ax^2+bx+c\), przechodzi przez punkt \((-2,10)\) oraz \(f(-1)=f(3)=0\). Oblicz odległość wierzchołka paraboli od początku układu współrzędnych.
Dana jest funkcja kwadratowa \(f(x)=ax^2+4x+1\). Wierzchołek paraboli, która jest wykresem tej funkcji, leży na prostej o równaniu \(y=-5\). Oblicz współrzędne tego wierzchołka.
Zbiorem wartości funkcji kwadratowej \(f(x)=-\frac{1}{3}x^2-2x+c\) jest przedział \((-\infty ,7\rangle \). Zatem współczynnik \(c\) jest równy
A.\( -3 \)
B.\( 4 \)
C.\( 7 \)
D.\( 10 \)
Największa wartość funkcji kwadratowej \(f(x)=a(x-2)^2-4\), gdzie \(a\ne 0\), w przedziale domkniętym \(\langle -4,-2\rangle \) jest równa \(12\). Wyznacz najmniejszą wartość funkcji \(f\) w przedziale \(\langle -4,-2\rangle \).
Funkcja kwadratowa \(f\), której miejscami zerowymi są liczby \(-2\) i \(4\), dla argumentu \(1\) przyjmuje wartość \(3\). Uzasadnij, że wykres funkcji \(f\) ma dwa punkty wspólne z prostą \(y=2\).
Wierzchołki trójkąta \(ABC\) leżą na paraboli, która jest wykresem pewnej funkcji kwadratowej \(f\) (zobacz rysunek).  Pole trójkąta jest równe \(8\), punkt \(C=(1,4)\) jest wierzchołkiem paraboli, a punkty \(A\) i \(B\) leżą na osi \(Ox\). Wyznacz wzór funkcji \(f\).
Pole trójkąta jest równe \(8\), punkt \(C=(1,4)\) jest wierzchołkiem paraboli, a punkty \(A\) i \(B\) leżą na osi \(Ox\). Wyznacz wzór funkcji \(f\).
 Pole trójkąta jest równe \(8\), punkt \(C=(1,4)\) jest wierzchołkiem paraboli, a punkty \(A\) i \(B\) leżą na osi \(Ox\). Wyznacz wzór funkcji \(f\).
Pole trójkąta jest równe \(8\), punkt \(C=(1,4)\) jest wierzchołkiem paraboli, a punkty \(A\) i \(B\) leżą na osi \(Ox\). Wyznacz wzór funkcji \(f\).W układzie współrzędnych na płaszczyźnie rysujemy łamane. Kolejne wierzchołki każdej z tych łamanych to punkty: \[A_1=(0,0),\quad A_2=(1,0),\quad A_3=(1,-1),\quad A_4=(-1,-1),\quad A_5=(-1,1),\quad A_6=(2,1)\] i tak dalej. Na rysunku jest przedstawiona łamana składająca się z dziesięciu odcinków, której ostatnim wierzchołkiem jest punkt \(A_{11}=(3,-3)\). Funkcja \(f\) przyporządkowuje każdej liczbie naturalnej \(n\ge 1\) długość łamanej złożonej z \(2n\) odcinków, czyli takiej, której początkowym wierzchołkiem jest punkt \(A_1\), a końcowym \(A_{2n+1}\). Wyznacz wzór funkcji \(f\) oraz oblicz jej wartość dla \(n=33\). 

Dany jest trójkąt prostokątny o kątach ostrych \(\alpha \) i \(\beta \), w którym \(\sin \alpha = \frac{\sqrt{6}}{3}\). Wtedy
A.\( \cos \alpha =\frac{\sqrt{3}}{2} \)
B.\( \cos \beta =\frac{\sqrt{6}}{3} \)
C.\( \operatorname{tg} \alpha =\frac{\sqrt{3}}{3} \)
D.\( \operatorname{tg} \beta =\frac{\sqrt{6}}{2} \)
Dana jest liczba \(a=\sin 72^\circ \). Zapisz liczbę \(1+\operatorname{tg}^2 72^\circ \) w zależności od \(a\).
Oblicz wartość wyrażenia \(\frac{2\sin \alpha -3\cos \alpha }{3\cos \alpha -5\sin \alpha }\), jeśli wiadomo, że \(\alpha \) jest kątem ostrym oraz \(\operatorname{tg} \alpha =3\).
Kąty \(\alpha \) i \(\beta \) są kątami ostrymi w trójkącie prostokątnym i \(\cos \alpha =\frac{2}{5}\). Oblicz \(\operatorname{tg} \alpha \cdot \sin \beta \).
Dla pewnego kąta ostrego \(\alpha \) funkcje trygonometryczne sinus i cosinus mają wartości \(\sin \alpha =a-\frac{1}{4}\), \(\cos \alpha =a+\frac{1}{4}\). Uzasadnij, że \(\operatorname{tg} \alpha =\frac{4-\sqrt{7}}{3}\).
Kąt \(\alpha \) jest kątem ostrym oraz \(\cos \alpha =\frac{2}{3}\). Wykaż, że średnia arytmetyczna liczb: \(a=\sin \alpha \), \(b=\frac{1}{2}\) oraz \(c=\frac{\operatorname{tg} \alpha }{3}\) jest równa \(\frac{\sqrt{5}+1}{6}\).
Wykaż, że jeżeli \(\alpha \) i \(\beta \) są kątami ostrymi takimi, że \(\sin \alpha =\frac{\sqrt{35}}{6}\) oraz \(\operatorname{tg} \beta =\sqrt{35}\), to \(\alpha =\beta \).
Funkcja wymierna \(f\) jest dana wzorem \(f(x)=\frac{x^2+2x-3}{x^2-3x-6}\). Wyznacz wszystkie wartości argumentu, dla których funkcja \(f\) przyjmuje wartość \(2\).
Najmniejszą wartością, jaką funkcja kwadratowa \(f\) dana wzorem \(f(x)=ax^2+bx+c\) przyjmuje w przedziale \(\langle 0,4\rangle \), jest \(f(2)\). Uzasadnij, że \(a\gt 0\) i \(b\lt 0\).
Funkcja kwadratowa \(f\) przyjmuje w przedziale \(\langle 0,3\rangle \) największą wartość dla argumentów \(0\) i \(3\). Uzasadnij, że w przedziale \(\langle -2,5\rangle \) funkcja \(f\) przyjmuje największą wartość dla argumentów \(-2\) i \(5\).
Oblicz sumę wszystkich parzystych liczb całkowitych dodatnich nie większych od \(1000\) i niepodzielnych przez \(3\).
W pewnym ciągu geometrycznym \(a_n\) wyraz \(a_4\) jest osiem razy większy od wyrazu \(a_1\). Drugi wyraz tego ciągu jest równy \(6\). Znajdź najmniejszą liczbę naturalną \(k\) taką, że \(a_k\gt 100\).
Trójwyrazowy ciąg \((x+1,x-1,2x)\) jest arytmetyczny dla
A.\( x=-3 \)
B.\( x=-1 \)
C.\( x=0 \)
D.\( x=2 \)
W ciągu arytmetycznym \(a_n\) dla \(n\ge 1\), \(a_1=8\) oraz \(a_1+a_2+a_3=33\). Wtedy suma \(a_4+a_5+a_6\) jest równa
A.\( 44 \)
B.\( 60 \)
C.\( 69 \)
D.\( 93 \)
Suma \(n\) początkowych wyrazów ciągu arytmetycznego \((a_n)\) dana jest wzorem \(S_n=\frac{n^2-25n}{4}\), gdzie \(n\ge 1\). Różnica ciągu arytmetycznego \((b_n)\) jest równa \(\frac{3}{2}\) oraz jego piąty wyraz jest równy \(8\). Wyznacz sumę \(17\) początkowych wyrazów ciągu arytmetycznego \((c_n)\), wiedząc, że \(c_n=2b_n-a_8\), gdzie \(n\ge 1\).
Suma \(23\) początkowych wyrazów ciągu arytmetycznego \((a_n)\) dla \(n\ge 1\) jest równa \(1564\). Oblicz średnią arytmetyczną wyrazów \(a_3\) i \(a_{21}\).
Dany jest ciąg arytmetyczny \((a_n)\) określony dla \(n\ge 1\). Wykaż, że ciąg \((b_n)\), określony dla \(n\ge 1\) wzorem ogólnym \(b_n=2a_{n+2}+4a_{n+4}\) jest arytmetyczny.
Skończony ciąg arytmetyczny ma nieparzystą liczbę wyrazów. Wszystkie wyrazy tego ciągu są liczbami całkowitymi. Uzasadnij, że środkowy wyraz jest dzielnikiem sumy tych wyrazów.
W ciągu geometrycznym rosnącym pierwszy wyraz jest równy \((-16)\), a siódmy wyraz jest równy \(\left(-\frac{1}{4}\right)\). Kwadrat czwartego wyrazu jest równy
A.\( -2 \)
B.\( 4 \)
C.\( \left(\frac{61}{8}\right)^2 \)
D.\( \left(\frac{65}{8}\right)^2 \)
W ciągu geometrycznym \((a_n)\), w którym \(a_1=1\), znane są wartości dwóch wyrazów: \(a_k=16\) i \(a_{k+2}=32\), gdzie \(k\) jest pewną liczbą całkowitą dodatnią. Wyznacz wyraz \(a_{10}\).
Kacper przez \(5\) dni zapisywał swoje wydatki. Zauważył, że każdego dnia wydatki były niższe o \(20\%\) w stosunku do wydatków poprzedniego dnia. Oblicz kwotę, jaką Kacper wydał w tym czasie, jeśli piątego dnia wydał \(20{,}48\) zł.
W ciągu geometrycznym \((a_n)\) o różnych i niezerowych wyrazach różnica między wyrazami piątym i trzecim jest trzy razy większa niż różnica między wyrazami czwartym i trzecim. Oblicz iloraz ciągu \((a_n)\).
Dany jest ciąg geometryczny \((a_n)\) o wszystkich wyrazach różnych od zera, określony dla \(n\ge 1\). Wykaż, że ciąg \((b_n)\), określony dla \(n\ge 1\) wzorem ogólnym \(b_n=a_n\cdot (2a_{n+2})^2\), jest geometryczny.
Dana jest funkcja wykładnicza \(f(x)=2^x\) oraz ciąg o wyrazie ogólnym \(a_n=f(3n)\), dla \(n\ge 1\). Wykaż, że ciąg \((a_n)\) jest geometryczny i oblicz iloraz tego ciągu.
Skończony ciąg \((a_1,a_2,a_3,a_4,a_5)\) jest geometryczny. Uzasadnij, że mając dany tylko wyraz środkowy \(a_3\), można obliczyć iloczyn wszystkich wyrazów tego ciągu.
Trójkąt ostrokątny \(ABC\) jest wpisany w okrąg o środku \(O\) i promieniu \(4\). Kąt \(CAB\) jest równy kątowi \(OCB\) oraz kąt \(CBA\) jest równy kątowi \(OCA\). Oblicz długość wysokości \(CD\) opuszczonej z wierzchołka \(C\) na bok \(AB\).
Podstawą ostrosłupa \(ABCDS\) jest romb o boku długości \(3\). Krawędź boczna \(DS\) ma długość \(4\) i jest jednocześnie wysokością tego ostrosłupa. Długości pozostałych trzech krawędzi bocznych są równe (zobacz rysunek).  Oblicz objętość tego ostrosłupa.
Oblicz objętość tego ostrosłupa.
 Oblicz objętość tego ostrosłupa.
Oblicz objętość tego ostrosłupa.Na rysunku jest przedstawiona prosta zawierająca przekątną \(AC\) rombu \(ABCD\) oraz wierzchołki \(A=(-2,1)\) i \(C=(4,5)\) tego rombu. 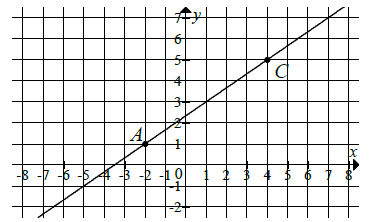 Wskaż równanie prostej zawierającej przekątną \(BD\) tego rombu.
Wskaż równanie prostej zawierającej przekątną \(BD\) tego rombu.
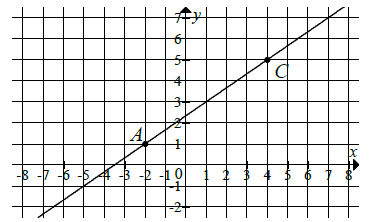 Wskaż równanie prostej zawierającej przekątną \(BD\) tego rombu.
Wskaż równanie prostej zawierającej przekątną \(BD\) tego rombu. A.\( y=-\frac{2}{3}x+\frac{11}{3} \)
B.\( y=-\frac{3}{2}x+4 \)
C.\( y=-x+4 \)
D.\( y=-\frac{3}{2}x+\frac{9}{2} \)
Odcinek \(AB\) jest średnicą okręgu o środku w punkcie \(O\) i promieniu r (zobacz rysunek).  Cięciwa \(AC\) ma długość \(r\sqrt{3}\), więc
Cięciwa \(AC\) ma długość \(r\sqrt{3}\), więc
 Cięciwa \(AC\) ma długość \(r\sqrt{3}\), więc
Cięciwa \(AC\) ma długość \(r\sqrt{3}\), więc A.\( |\sphericalangle AOC|=130^\circ \)
B.\( |\sphericalangle ABC|=90^\circ \)
C.\( |\sphericalangle BOC|=60^\circ \)
D.\( |\sphericalangle BAC|=45^\circ \)
Punkty \(A\), \(B\), \(C\), \(D\), \(E\) są położone w tej kolejności na okręgu o środku \(O\) (zobacz rysunek). Odcinki \(BD\) i \(AC\) są średnicami tego okręgu oraz \(|\sphericalangle BEC|=60^\circ \). Oblicz miarę kąta \(CBD\). 

Punkty \(A\), \(B\), \(C\), \(D\) są położone w tej kolejności na okręgu o środku \(O\) (zobacz rysunek). Odcinek \(DB\) jest średnicą tego okręgu i \(|\sphericalangle BAC|=\alpha \), \(|\sphericalangle CBD|=\beta \). Wykaż, że \(\alpha +\beta =90^\circ \). 

Parami różne punkty \(A\), \(B\), \(C\), \(D\), \(E\) leżą na okręgu. Odcinki \(DE\) i \(AC\) są równoległe, zaś odcinek \(BD\) jest średnicą tego okręgu (zobacz rysunek). Wykaż, że prosta \(BE\) zawiera wysokość trójkąta \(ABC\) opuszczoną na bok \(AC\). 

Końce odcinka \(AB\) o długości \(9\) są środkami okręgów o promieniach \(6\) i \(4\) (zobacz rysunek).  Punkt \(C\) leży na odcinku \(AB\) i jest środkiem takiego okręgu, o promieniu większym od \(6\), że dwa dane okręgi są do niego wewnętrznie styczne. Promień okręgu o środku \(C\) ma długość
Punkt \(C\) leży na odcinku \(AB\) i jest środkiem takiego okręgu, o promieniu większym od \(6\), że dwa dane okręgi są do niego wewnętrznie styczne. Promień okręgu o środku \(C\) ma długość
 Punkt \(C\) leży na odcinku \(AB\) i jest środkiem takiego okręgu, o promieniu większym od \(6\), że dwa dane okręgi są do niego wewnętrznie styczne. Promień okręgu o środku \(C\) ma długość
Punkt \(C\) leży na odcinku \(AB\) i jest środkiem takiego okręgu, o promieniu większym od \(6\), że dwa dane okręgi są do niego wewnętrznie styczne. Promień okręgu o środku \(C\) ma długość A.\( 6{,}5 \)
B.\( 7{,}5 \)
C.\( 8{,}5 \)
D.\( 9{,}5 \)
Dwa okręgi o promieniach \(r\) i \(R\) są styczne zewnętrznie i są styczne do wspólnej prostej w punktach \(A\) i \(B\) (zobacz rysunek). Oblicz wartość iloczynu \(rR\), jeżeli wiadomo, że odcinek \(AB\) ma długość \(5\). 

Dane są dwa okręgi styczne wewnętrznie: okrąg \(O_1\) o środku \(S\) i promieniu równym \(6\) oraz okrąg \(O_2\) o środku \(T\) i promieniu długości \(2\). Z punktu \(S\) poprowadzono półproste styczne do okręgu \(O_2\) w punktach \(K\) i \(L\). Oblicz pole czworokąta \(SKTL\).
Pole trójkąta \(ABC\) równe jest \(S\). Każdy bok trójkąta podzielono w stosunku \(x : y : x\), gdzie \(x\) i \(y\) są pewnymi liczbami dodatnimi. Wyznacz pole sześciokąta, którego wierzchołkami są punkty podziałów boków trójkąta (zobacz rysunek). 

Odcinki \(AD\) i \(BE\) przecinają się w punkcie \(C\). W trójkątach \(ABC\) i \(CDE\) zachodzą związki: \(|\sphericalangle CAB|=|\sphericalangle CED|\), \(|AC|=5\), \(|BC|=3\), \(|CE|=10\) (zobacz rysunek). Wykaż, że trójkąty \(ABC\) i \(CDE\) są podobne. Oblicz długość boku \(CD\). 

Dany jest trójkąt prostokątny \(ABC\), w którym przyprostokątna \(AC\) ma długość \(12\). Punkt \(E\) jest środkiem przeciwprostokątnej \(AB\), spodek \(D\) wysokości \(CD\) leży między punktami \(A\) i \(E\), a odległość między punktami \(D\) i \(E\) jest równa \(1\) (zobacz rysunek). Oblicz obwód tego trójkąta. 

Na rysunku przedstawiono trapez \(ABCD\) oraz zaznaczono wysokości \(DE\) i \(CF\) tego trapezu. Punkt \(F\) jest środkiem podstawy \(AB\), a punkt \(E\) dzieli tę podstawę w stosunku \(2:5\). Wykaż, że punkt przecięcia wysokości \(CF\) z przekątną \(DB\) dzieli tę przekątną w stosunku \(3:7\), licząc od wierzchołka \(D\). 

W trójkącie \(ABC\) o bokach długości \(|AC|=b\), \(|BC|=a\) i kącie między nimi \(60^\circ \) poprowadzono dwusieczną kąta \(ACB\), która przecięła bok \(AB\) w punkcie \(D\). Zapisz długość odcinka \(CD\) w zależności od \(a\) i \(b\).
Dany jest trapez prostokątny \(ABCD\) taki, że kąty przy wierzchołkach \(A\) i \(D\) są proste oraz \(|AB|=10\), \(|DC|=6\), a przekątna \(AC\) jest dwa razy dłuższa od ramienia \(DA\). Na podstawie \(AB\) obrano taki punkt \(X\), że \(|CX|=|CB|\) (zobacz rysunek). Oblicz sinus kąta \(XCB\). 

Wyznacz współrzędne środka okręgu opisanego na kwadracie, którego jeden z boków jest zawarty w prostej o równaniu \(y=2x-2\), a punkt \(A=(1,5)\) jest jego wierzchołkiem. Rozważ wszystkie przypadki.
Dwa boki trójkąta prostokątnego \(ABC\) są zawarte w prostych o równaniach \(y = 2x − 3\) oraz \(y=\frac{1}{4}x-\frac{5}{4}\). Wyznacz równanie prostej, która przechodzi przez punkt \(K=(4,-2)\) i zawiera trzeci bok trójkąta \(ABC\). Rozważ wszystkie możliwości.
Różnica współczynników kierunkowych dwóch prostych jest równa różnicy odwrotności tych współczynników. Uzasadnij, że te proste są prostopadłe albo równoległe.
Punkty \(A\) i \(B\), których pierwsze współrzędne są równe odpowiednio \(−2\) i \(2\), należą do wykresu funkcji \(f(x)=-\frac{8}{x}+3\). Oblicz współrzędne punktu \(C\), wiedząc, że punkt \(B\) jest środkiem odcinka \(AC\).
Prosta \(l\) przecina okrąg o środku \(S\) w punktach \(A=\left(1-\sqrt{2},-\frac{1}{8}\right)\) i \(B=\left(1+\sqrt{2},-\frac{3}{8}\right)\). Punkt \(S\) leży na prostej \(l\). Sprawdź, czy punkt \(S\) leży na prostej \(k\) o równaniu \(x − 4 y = 0\).
Dany jest sześciokąt foremny \(ABCDEF\), którego środkiem symetrii jest punkt \(O=(3,-\sqrt{3})\), a wierzchołek \(A\) ma współrzędne \(A=(1,-3\sqrt{3})\). Wiadomo, że punkt \(P=(4,-2\sqrt{3})\) jest środkiem odcinka \(BO\). Oblicz współrzędne pozostałych wierzchołków tego sześciokąta.
Punkt \(M=(2,1)\) jest środkiem boku \(AB\), a punkt \(N=(8,3)\) to środek boku \(BC\) kwadratu \(ABCD\). Oblicz długość boku kwadratu \(ABCD\).
Trójkąt o wierzchołkach \(A=(-6,0)\), \(B=(6,4)\) i \(C=(-3,-8)\) przekształcono przez symetrię środkową względem początku układu współrzędnych i otrzymano trójkąt \(A_1B_1C_1\). Oblicz sumę kątów wewnętrznych wielokąta, który jest częścią wspólną trójkąta \(ABC\) i jego obrazu, tj. \(A_1B_1C_1\).
Prosta \(y = 0\) jest osią symetrii figury złożonej z dwóch prostych o równaniach \(y=(p+2)x-q\) i \(y=(q-5)x+2p\). Wyznacz \(p\) i \(q\). Narysuj te proste w układzie współrzędnych.
Dany jest trapez równoramienny \(ABCD\), niebędący równoległobokiem, w którym \(AB||CD\) oraz \(A=(-9,7)\), \(B=(3,1)\), \(D=(-3,10)\). Trapez \(A_1B_1C_1D_1\) jest obrazem trapezu \(ABCD\) w symetrii środkowej względem początku układu współrzędnych. Wyznacz współrzędne wierzchołków trapezu \(A_1B_1C_1D_1\) oraz równanie osi symetrii tego trapezu.
Punkt \(P\) leży wewnątrz trójkąta o wierzchołkach \(A=(6,0)\), \(B=(0,4)\), \(C=(0,0)\). Oznaczmy przez \(P_{AC}\) obraz punktu \(P\) w symetrii osiowej względem prostej \(AC\), a przez \(P_{BC}\) obraz punktu \(P\) w symetrii osiowej względem prostej \(BC\). Uzasadnij, że punkty \(P_{AC}\), \(C\) i \(P_{BC}\) leżą na jednej prostej.
Przedstawiona na rysunku bryła składa się z walca i półkuli. Wysokość walca jest taka, jak promień jego podstawy i jest równa \(R\).  Objętość tej bryły jest równa
Objętość tej bryły jest równa
 Objętość tej bryły jest równa
Objętość tej bryły jest równa A.\( \pi R^3 \)
B.\( \frac{5}{3}\pi R^3 \)
C.\( \frac{2}{3}\pi R^3 \)
D.\( 2\pi R^3 \)
Podstawą graniastosłupa prostego czworokątnego \(ABCDEFGH\) jest kwadrat \(ABCD\) (zobacz rysunek).  Kąt \(AHC\) między przekątnymi sąsiednich ścian bocznych ma \(50^\circ \). Kąt \(DBG\) między przekątną podstawy a przekątną ściany bocznej jest równy
Kąt \(AHC\) między przekątnymi sąsiednich ścian bocznych ma \(50^\circ \). Kąt \(DBG\) między przekątną podstawy a przekątną ściany bocznej jest równy
 Kąt \(AHC\) między przekątnymi sąsiednich ścian bocznych ma \(50^\circ \). Kąt \(DBG\) między przekątną podstawy a przekątną ściany bocznej jest równy
Kąt \(AHC\) między przekątnymi sąsiednich ścian bocznych ma \(50^\circ \). Kąt \(DBG\) między przekątną podstawy a przekątną ściany bocznej jest równy A.\( 60^\circ \)
B.\( 65^\circ \)
C.\( 75^\circ \)
D.\( 80^\circ \)
Dany jest ostrosłup prawidłowy czworokątny \(ABCDS\), którego ściany boczne są trójkątami równobocznymi. Punkty \(G\), \(E\) i \(F\) są odpowiednio środkami odcinków \(AD\), \(BC\) i \(CS\) (zobacz rysunek).  Kątem między przeciwległymi ścianami bocznymi jest kąt
Kątem między przeciwległymi ścianami bocznymi jest kąt
 Kątem między przeciwległymi ścianami bocznymi jest kąt
Kątem między przeciwległymi ścianami bocznymi jest kąt A.\( DFE \)
B.\( GES \)
C.\( ESG \)
D.\( ASC \)
Wysokość graniastosłupa prawidłowego trójkątnego \(ABCDEF\) (zobacz rysunek) jest równa \(8\), a tangens kąta między wysokością trójkąta \(ABF\) poprowadzoną z wierzchołka \(F\) i płaszczyzną podstawy \(ABC\) tego graniastosłupa jest równy \(\frac{4\sqrt{3}}{3}\). Oblicz pole trójkąta \(ABF\). 

Objętość graniastosłupa prawidłowego trójkątnego, w którym krawędź podstawy ma długość \(4\), jest równa \(16\sqrt{6}\) (zobacz rysunek). Oblicz miarę kąta nachylenia przekątnej ściany bocznej do sąsiedniej ściany bocznej. 

W graniastosłupie prawidłowym sześciokątnym krótsza przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem \(\beta \) takim, że \(\sin \beta =\frac{2}{\sqrt{7}}\). Oblicz miarę kąta \(\alpha \), jaki tworzy dłuższa przekątna tej bryły z płaszczyzną podstawy. 

Dany jest ostrosłup prawidłowy trójkątny o krawędzi podstawy długości \(6\sqrt{3}\) oraz krawędzi bocznej długości \(12\). Wyznacz miarę kąta między ścianami bocznymi tego ostrosłupa. Wynik podaj z dokładnością do \(2^\circ \).
W ostrosłupie prawidłowym czworokątnym kąt pomiędzy wysokością ostrosłupa a wysokością ściany bocznej jest równy \(30^\circ \). Promień okręgu opisanego na podstawie jest równy \(2\sqrt{2}\). Oblicz sinus kąta nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy.
W stożku stosunek pola powierzchni bocznej do pola podstawy jest równy \(\frac{3}{2}\). Oblicz sinus kąta między tworzącą a płaszczyzną podstawy tego stożka.
W trójkącie \(ABC\) punkt \(D\) jest środkiem boku \(AB\) oraz \(|CD|=|CB|\) (zobacz rysunek). Bok \(CB\) przedłużono tak, że \(|CB|=|BE|\). Wykaż, że \(|AC|=|DE|\). 

Tworząca stożka o kącie rozwarcia \(\alpha \) ma długość \(8\). Pole powierzchni całkowitej tego stożka jest równe \(48\pi\). Oblicz objętość stożka oraz miarę kąta \(\alpha \).
Dany jest graniastosłup prawidłowy czworokątny \(ABCDEFGH\) o krawędzi podstawy długości \(4\sqrt{2}\) oraz krawędzi bocznej równej \(8\). Graniastosłup przecięto płaszczyzną przechodzącą przez środki krawędzi \(AD\) i \(DC\) oraz przez wierzchołek \(H\) (zobacz rysunek). Oblicz pole otrzymanego przekroju. 

W sześcianie \(ABCDA_1B_1C_1D_1\) przekątna \(AC_1\) tworzy z płaszczyzną \(ABCD\) kąt \(\alpha \). Punkty \(L\) i \(J\) są odpowiednio środkami krawędzi \(DD_1\) i \(BB_1\) oraz \(|\sphericalangle LAJ|=2\beta \). Uzasadnij, że \(cos\alpha =\operatorname{tg} \beta \).
W ostrosłupie prawidłowym trójkątnym krawędź podstawy jest \(2\) razy dłuższa od wysokości ostrosłupa poprowadzonej na tę podstawę. Wyznacz kąt nachylenia ściany bocznej do podstawy.
Dany jest ostrosłup prawidłowy czworokątny, którego wysokość ma długość \(H\) oraz kąt między krawędzią boczną i płaszczyzną podstawy jest równy \(60^\circ \). Wyznacz wzór na pole powierzchni bocznej tego ostrosłupa w zależności od wysokości \(H\).
W stożku różnica długości tworzącej i promienia podstawy jest równa \(6\). Cosinus kąta \(\alpha \) między tworzącą a płaszczyzną podstawy tego stożka jest równy \(\frac{2}{5}\). Oblicz pole powierzchni bocznej tego stożka.
Graniastosłup prawidłowy czworokątny \(ABCDEFGH\) o krawędzi podstawy długości \(5\) oraz krawędzi bocznej długości \(5\sqrt{6}\) przecięto płaszczyzną przechodzącą przez wierzchołek \(A\) oraz punkty \(L\) oraz \(J\) leżące na przeciwległych krawędziach bocznych w równych odległościach od dolnej podstawy. Otrzymany przekrój jest czworokątem \(AJKL\), którego przekątna \(AK\) tworzy z płaszczyzną podstawy kąt \(\alpha \) (zobacz rysunek). Zapisz pole tego przekroju w zależności od kąta \(\alpha \). Jakie wartości przyjmuje \(\alpha \)? 

Dana jest prosta o równaniu \(y=-\frac{1}{2}x+b\), gdzie \(b\gt 0\) przecina oś \(Oy\) w punkcie \(A\), zaś oś \(Ox\) w punkcie \(B\) (zobacz rysunek). Pole trójkąta \(AOB\) wyznaczonego przez tę prostą i osie układu współrzędnych jest równe 1\(\)6. Oblicz współrzędne środka okręgu opisanego na trójkącie \(AOB\). 

Punkty \(A=(7,6)\) i \(B=(1,-2)\) są wierzchołkami trójkąta równobocznego \(ABC\). Promień koła opisanego na tym trójkącie jest równy
A.\( \frac{5\sqrt{3}}{6} \)
B.\( \frac{5\sqrt{3}}{3} \)
C.\( \frac{10\sqrt{3}}{6} \)
D.\( \frac{10\sqrt{3}}{3} \)
Trójkąt \(T\) jest podobny do trójkąta \(T_1\) w skali \(k=\frac{1}{6}\), a trójkąt \(T_2\) jest podobny do trójkąta \(T\) w skali \(k=3\). Pole trójkąta \(T_2\) jest równe \(24\). Trójkąt \(T_1\) ma pole równe
A.\( 12 \)
B.\( 48 \)
C.\( 72 \)
D.\( 96 \)
Punkt \(A=(2,7)\) jest wierzchołkiem kwadratu \(ABCD\), a punkt \(S=(6,5)\) jest środkiem okręgu opisanego na tym kwadracie. Bok tego kwadratu ma długość
A.\( \sqrt{10} \)
B.\( \sqrt{20} \)
C.\( 2\sqrt{10} \)
D.\( 2\sqrt{20} \)
W trójkącie prostokątnym \(ABC\) kąt przy wierzchołku \(A\) jest prosty oraz \(\sin (\sphericalangle ABC)=\frac{1}{3}\). Oblicz \(\operatorname{tg} (\sphericalangle ABC)\).
Do okręgu o środku \(O\) poprowadzono z zewnętrznego punktu \(P\) dwie styczne przecinające się w \(P\) pod kątem \(50^\circ \) (zobacz rysunek). Punktami styczności są, odpowiednio, punkty \(A\) i \(B\).  Kąt \(AOB\) ma miarę
Kąt \(AOB\) ma miarę
 Kąt \(AOB\) ma miarę
Kąt \(AOB\) ma miarę A.\( 90^\circ \)
B.\( 120^\circ \)
C.\( 130^\circ \)
D.\( 150^\circ \)
Na płaszczyźnie dane są trzy punkty: \(A=(-1,1)\), \(B=(5,-3)\) oraz \(C=(3,2)\). Wyznacz równanie środkowej poprowadzonej do boku \(AB\) w trójkącie \(ABC\).
Wykres funkcji kwadratowej \(f\) danej wzorem \(f(x)=2x^2-5x+3\) przecięto prostymi o równaniach \(x=-1\) oraz \(x=2\). Oblicz odległość między punktami przecięcia tych prostych z wykresem funkcji \(f\).
Niech prosta \(k\) będzie dana równaniem \(y=2x+1\). Uzasadnij, że jej obrazem w symetrii środkowej względem początku układu współrzędnych jest prosta do niej równoległa.
W pojemniku jest \(10\) kul, w tym \(b\) kul białych i \(10-b\) kul czarnych, gdzie \(b\ne 5\). Z tego pojemnika losujemy dwa razy po jednej kuli ze zwracaniem. Wykaż, że prawdopodobieństwo zdarzenia polegającego na tym, że otrzymamy dwie kule tego samego koloru, jest większe od \(\frac{1}{2}\).
Wykonano pomiary wysokości czterech krzeseł i każde dwa rezultaty były różne. Adam zapisał wyniki w metrach i odchylenie standardowe jego danych było równe \(\sigma _A\). Bogdan zapisał te wyniki w centymetrach i odchylenie standardowe jego danych było równe \(\sigma _B\). Wynika stąd, że
A.\( \sigma _A=10\sigma _B \)
B.\( \sigma _A = 100\sigma _B \)
C.\( 10\sigma _A=\sigma _B \)
D.\( 100\sigma _A=\sigma _B \)
Dany jest zbiór \(A=\{1,2,...,2n,2n+1\}\), gdzie \(n\ge 1\), złożony z \(2n+1\) kolejnych liczb naturalnych. Wykaż, że liczba wszystkich par \((a,b)\) takich, że \(a\in A\), \(b\in A\) i \(a\ne b\) oraz suma \(a+b\) jest nieparzysta, jest większa od liczby par, których suma jest parzysta.
Rzucono \(100\) razy sześcienną kostką do gry. Średnia arytmetyczna liczb oczek w pierwszych \(40\) rzutach była równa \(3{,}75\), a średnia arytmetyczna liczb oczek w kolejnych \(60\) rzutach była równa \(4{,}25\). Średnia arytmetyczna liczb oczek w \(100\) rzutach jest
A.mniejsza od \( 4 \)
B.równa \( 4 \)
C.równa \( 4{,}05 \)
D.większa od \( 4{,}05 \)
Zestaw danych: \(x_1,x_2,x_3,...,x_n\) ma średnią arytmetyczną \(a\) i odchylenie standardowe \(s\). Wykaż, że zestaw danych: \(\frac{x_1-a}{s}, \frac{x_2-a}{s}, \frac{x_3-a}{s},...,\frac{x_n-a}{s}\) ma średnią arytmetyczną \(0\).
Adam otrzymał z trzech kolejnych klasówek następujące oceny: \(6\), \(4\), \(4\). Oblicz, jaką ocenę otrzymał Adam z czwartej klasówki, jeżeli odchylenie standardowe otrzymanych ocen jest równe \(\sqrt{\frac{11}{16}}\).
Wszystkich par \((a,b)\) takich, że \(a\in \{1,2,3,4,5,6,7\}\) i \(b\in \{1,2,3,4,5,6,7,8,9\}\) oraz suma \(a+b\) jest podzielna przez \(3\), jest
A.mniej niż \( 21 \)
B.dokładnie \( 21 \)
C.dokładnie \( 22 \)
D.więcej niż \( 22 \)
Liczb ze zbioru \(Z=\{1,2,3,...,36\}\), których nie można uzyskać jako iloczynu dwóch niekoniecznie różnych liczb ze zbioru \(\{1,2,3,...,6\}\), jest
A.\( 8 \)
B.\( 16 \)
C.\( 18 \)
D.\( 19 \)
Liczb naturalnych trzycyfrowych, w zapisie których każda cyfra występuje co najwyżej raz oraz suma cyfry setek i cyfry jedności jest równa \(4\), jest
A.mniej niż \( 24 \)
B.dokładnie \( 24 \)
C.dokładnie \( 32 \)
D.więcej niż \( 32 \)
Ile jest wszystkich trzycyfrowych liczb naturalnych, w zapisie których każda cyfra jest inna, żadna nie jest zerem oraz jedną z cyfr jest dziewiątka?
A.\( 56 \)
B.\( 168 \)
C.\( 216 \)
D.\( 504 \)
Dana jest tabela złożona z sześciu wierszy i dziewięciu kolumn (zobacz rysunek). Oblicz, ile w tej tabeli można narysować, zgodnie z zaznaczonymi liniami, prostokątnych tabel o czterech wierszach i czterech kolumnach. 

Wszystkie losy loterii fantowej zostały ponumerowane kolejno od numeru \(10000\) do numeru \(99999\). Te losy, którym nadano numery o sumie cyfr równej trzy, są wygrywające, pozostałe losy są przegrywające. Na tej loterii będziemy losować jeden los. Oblicz prawdopodobieństwo wyciągnięcia losu przegrywającego. Wynik przedstaw w postaci ułamka dziesiętnego w przybliżeniu do czwartego miejsca po przecinku.
Na rysunku jest przedstawiony trzynastokąt wypukły o kolejnych wierzchołkach od \(A_1\) do \(A_{13}\) oraz przekątna \(A_1A_8\) tego wielokąta.  Spośród wszystkich \(65\) przekątnych tego wielokąta losujemy jedną. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana przekątna będzie przecinała się z przekątną \(A_1A_8\) w punkcie leżącym wewnątrz trzynastokąta. Wynik zapisz w postaci ułamka nieskracalnego.
Spośród wszystkich \(65\) przekątnych tego wielokąta losujemy jedną. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana przekątna będzie przecinała się z przekątną \(A_1A_8\) w punkcie leżącym wewnątrz trzynastokąta. Wynik zapisz w postaci ułamka nieskracalnego.
 Spośród wszystkich \(65\) przekątnych tego wielokąta losujemy jedną. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana przekątna będzie przecinała się z przekątną \(A_1A_8\) w punkcie leżącym wewnątrz trzynastokąta. Wynik zapisz w postaci ułamka nieskracalnego.
Spośród wszystkich \(65\) przekątnych tego wielokąta losujemy jedną. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana przekątna będzie przecinała się z przekątną \(A_1A_8\) w punkcie leżącym wewnątrz trzynastokąta. Wynik zapisz w postaci ułamka nieskracalnego.Spośród wierzchołków sześcianu wybieramy losowo dwa różne wierzchołki. Oblicz prawdopodobieństwo wylosowania wierzchołków, które są końcami tej samej przekątnej ściany sześcianu.
Ze zbioru wszystkich krawędzi (krawędzi bocznych i krawędzi podstawy) ostrosłupa prawidłowego pięciokątnego losujemy jedną krawędź, a następnie z pozostałych krawędzi losujemy drugą. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosowane krawędzie będą miały wspólny wierzchołek.
Tematy nadrzędne i sąsiednie