Matura podstawowa - kurs - część 58 - zadania

Drukuj

Poziom podstawowy

Cały kurs na: http://www.matemaks.pl/matematyka-matura-podstawowa-kurs.html.

Sześcian o krawędzi \(6\) przecięto płaszczyzną zawierającą przekątną dolnej podstawy i jeden wierzchołek drugiej (patrz rysunek). Oblicz pole otrzymanego przekroju.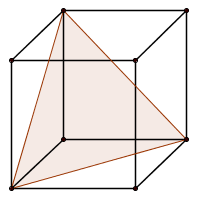

\(P=18\sqrt{3}\)

Dany jest graniastosłup prawidłowy czworokątny \(ABCDEFGH\) o krawędzi podstawy długości \(4\sqrt{2}\) oraz krawędzi bocznej równej \(8\). Graniastosłup przecięto płaszczyzną przechodzącą przez środki krawędzi \(AD\) i \(DC\) oraz przez wierzchołek \(H\) (zobacz rysunek). Oblicz pole otrzymanego przekroju.

\(4\sqrt{17}\)

Graniastosłup prawidłowy czworokątny \(ABCDEFGH\) o krawędzi podstawy długości \(5\) oraz krawędzi bocznej długości \(5\sqrt{6}\) przecięto płaszczyzną przechodzącą przez wierzchołek \(A\) oraz punkty \(L\) oraz \(J\) leżące na przeciwległych krawędziach bocznych w równych odległościach od dolnej podstawy. Otrzymany przekrój jest czworokątem \(AJKL\), którego przekątna \(AK\) tworzy z płaszczyzną podstawy kąt \(\alpha \) (zobacz rysunek). Zapisz pole tego przekroju w zależności od kąta \(\alpha \). Jakie wartości przyjmuje \(\alpha \)?

\(\frac{25}{\cos \alpha }\)