Matura podstawowa - kurs - część 56 - zadania

Cały kurs na: http://www.matemaks.pl/matematyka-matura-podstawowa-kurs.html.

Objętość walca o wysokości \(8\) jest równa \(72\pi\). Promień podstawy tego walca jest równy

A.\( 9 \)

B.\( 8 \)

C.\( 6 \)

D.\( 3 \)

Objętość walca, w którym wysokość jest trzykrotnie dłuższa od promienia podstawy, jest równa \( 24\pi \). Zatem promień podstawy tego walca ma długość

A.\(4 \)

B.\(8 \)

C.\(2 \)

D.\(6 \)

Jeżeli wysokość stożka zwiększymy trzykrotnie, a długość promienia zmniejszymy trzy razy, to objętość nowego stożka:

A.zwiększy się trzy razy

B.zmniejszy się trzy razy

C.zmniejszy się dziewięć razy

D.nie zmieni się

Stożek i walec mają takie same podstawy i równe pola powierzchni bocznych. Wtedy tworząca stożka jest

A.sześć razy dłuższa od wysokości walca

B.trzy razy dłuższa od wysokości walca

C.dwa razy dłuższa od wysokości walca

D.równa wysokości walca

Pole powierzchni całkowitej walca, którego przekrojem osiowym jest kwadrat o boku długości \( 4 \), jest równe

A.\(256\pi \)

B.\(128\pi \)

C.\(48\pi \)

D.\(24\pi \)

Tworząca stożka ma długość \( 17 \), a wysokość stożka jest krótsza od średnicy jego podstawy o \( 22 \). Oblicz pole powierzchni całkowitej i objętość tego stożka.

\(P=480\pi \), \(V=600\pi \)

Tworząca stożka ma długość \(l\), a promień jego podstawy jest równy \(r\).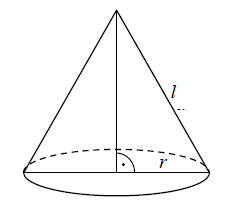

Powierzchnia boczna tego stożka jest \(2\) razy większa od pola jego podstawy. Wówczas

A.\( r=\frac{1}{6}l \)

B.\( r=\frac{1}{4}l \)

C.\( r=\frac{1}{3}l \)

D.\( r=\frac{1}{2}l \)

Prostokąt o bokach długości \(2\) i \(4\) obracamy wokół krótszego boku. Ile wynosi pole powierzchni całkowitej tak otrzymanej bryły?

A.\( 16\pi \)

B.\( 24\pi \)

C.\( 32\pi \)

D.\( 48\pi \)

Przekrojem osiowym stożka jest trójkąt równoboczny o boku długości \(6\). Objętość tego stożka jest równa

A.\( 6\pi \)

B.\( 18\pi \)

C.\( 9\pi\sqrt{3} \)

D.\( 27\pi\sqrt{3} \)

Dany jest trójkąt prostokątny o długościach boków \(a, b, c\), gdzie \(a \lt b \lt c\). Obracając ten trójkąt wokół prostej zawierającej dłuższą przyprostokątną o kąt \(360^\circ \) otrzymujemy bryłę, której objętość jest równa

A.\( V=\frac{1}{3}a^2b\pi \)

B.\( V=a^2b\pi \)

C.\( V=\frac{1}{3}b^2a\pi \)

D.\( V=a^2\pi +\pi ac \)

Przekątna przekroju osiowego walca, którego promień podstawy jest równy \(4\) i wysokość jest równa \(6,\) ma długość

A.\( \sqrt{10} \)

B.\( \sqrt{20} \)

C.\( \sqrt{52} \)

D.\( 10 \)

Przedstawiona na rysunku bryła składa się z walca i półkuli. Wysokość walca jest taka, jak promień jego podstawy i jest równa \(R\).

Objętość tej bryły jest równa

A.\( \pi R^3 \)

B.\( \frac{5}{3}\pi R^3 \)

C.\( \frac{2}{3}\pi R^3 \)

D.\( 2\pi R^3 \)

W stożku stosunek pola powierzchni bocznej do pola podstawy jest równy \(\frac{3}{2}\). Oblicz sinus kąta między tworzącą a płaszczyzną podstawy tego stożka.

\(\frac{\sqrt{5}}{3}\)

Tworząca stożka o kącie rozwarcia \(\alpha \) ma długość \(8\). Pole powierzchni całkowitej tego stożka jest równe \(48\pi\). Oblicz objętość stożka oraz miarę kąta \(\alpha \).

\(\alpha =60^\circ \) i \(V=\frac{64\pi \sqrt{3}}{3}\)

W stożku różnica długości tworzącej i promienia podstawy jest równa \(6\). Cosinus kąta \(\alpha \) między tworzącą a płaszczyzną podstawy tego stożka jest równy \(\frac{2}{5}\). Oblicz pole powierzchni bocznej tego stożka.

\(40\pi \)