Matura podstawowa - kurs - część 50 - zadania
Poziom podstawowy
Cały kurs na: http://www.matemaks.pl/matematyka-matura-podstawowa-kurs.html.Interpretację geometryczną układu równań \[\begin{cases} x-y=2\\ -2x+2y=4 \end{cases} \] przedstawiono na rysunku: 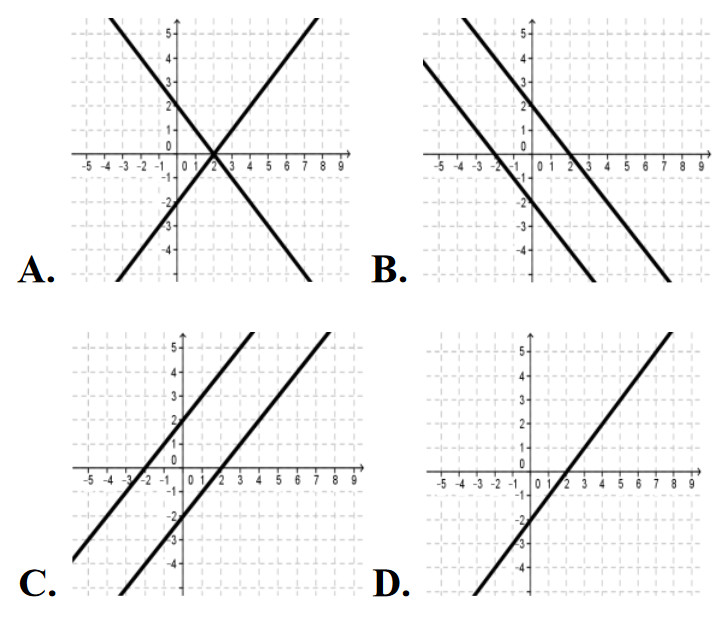

Rozwiązaniem układu równań \(\begin{cases} x+3y=5\\ 2x-y=3 \end{cases} \) jest
A.\( \begin{cases}x=2\\y=1 \end{cases} \)
B.\( \begin{cases}x=2\\y=-1 \end{cases} \)
C.\( \begin{cases}x=1\\y=2 \end{cases} \)
D.\( \begin{cases}x=1\\y=-2 \end{cases} \)
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.  Wskaż ten układ.
Wskaż ten układ.
 Wskaż ten układ.
Wskaż ten układ. A.\(\begin{cases} {y=x-1}\\ {y=-2x+4} \end{cases} \)
B.\(\begin{cases} {y=x-1}\\ {y=2x+4} \end{cases} \)
C.\(\begin{cases} {y=x+1}\\ {y=-2x+4} \end{cases} \)
D.\(\begin{cases} {y=x+1}\\ {y=2x+4} \end{cases} \)
Układ równań \(\begin{cases} y=3x+2 \\ y=(m-2)x+5 \end{cases} \) nie ma rozwiązań, gdy
A.\( m=2 \)
B.\( m=3 \)
C.\( m=4 \)
D.\( m=5 \)
Układ równań \(\begin{cases} x-y=3 \\ 2x+0{,}5y=4 \end{cases} \) opisuje w układzie współrzędnych na płaszczyźnie
A.zbiór nieskończony.
B.dokładnie 2 różne punkty.
C.dokładnie jeden punkt.
D.zbiór pusty.
Na jednym z poniższych rysunków przedstawiono interpretację geometryczną układu równań \[\begin{cases} x+3y=-5 \\ 3x-2y=-4 \end{cases} \] Wskaż ten rysunek. 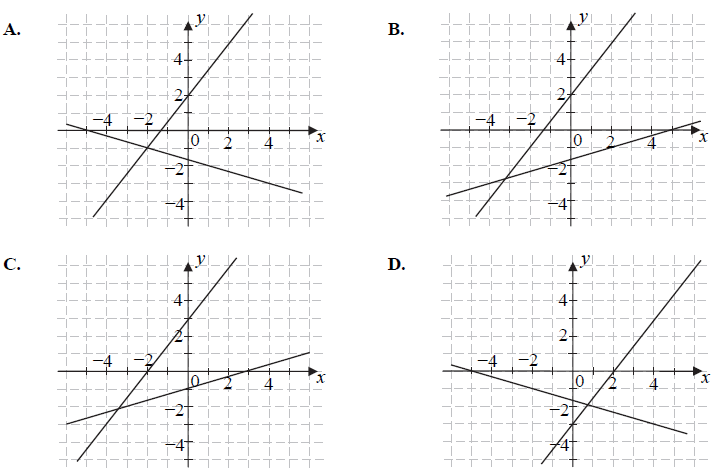

Tematy nadrzędne