Matura podstawowa - kurs - część 43 - zadania

Drukuj

Poziom podstawowy

Cały kurs na: http://www.matemaks.pl/matematyka-matura-podstawowa-kurs.html.

Kąt środkowy i kąt wpisany są oparte na tym samym łuku. Suma ich miar jest równa \( 180^\circ \). Jaka jest miara kąta środkowego?

A.\(60^\circ \)

B.\(90^\circ \)

C.\(120^\circ \)

D.\(135^\circ \)

Punkty \(A, B, C, D\) dzielą okrąg na \(4\) równe łuki. Miara zaznaczonego na rysunku kąta wpisanego \(ACD\) jest równa

A.\( 90^\circ \)

B.\( 60^\circ \)

C.\( 45^\circ \)

D.\( 30^\circ \)

Punkty \(A\) i \(B\) leżą na okręgu o środku \(O\) i dzielą ten okrąg na dwa łuki, których stosunek długości jest równy \(7:5\). Oblicz miarę kąta środkowego opartego na krótszym łuku.

\(150^\circ \)

Punkt \(O\) jest środkiem okręgu o średnicy \(AB\) (tak jak na rysunku). Kąt \(\alpha \) ma miarę

A.\( 40^\circ \)

B.\( 50^\circ \)

C.\( 60^\circ \)

D.\( 80^\circ \)

Punkt \(O\) jest środkiem okręgu. Kąt \(\alpha\), zaznaczony na rysunku, ma miarę

A.\( 50^\circ \)

B.\( 45^\circ \)

C.\( 25^\circ \)

D.\( 20^\circ \)

Kąt środkowy oparty na łuku, którego długość jest równa \( \frac{4}{9} \) długości okręgu, ma miarę

A.\(160^\circ \)

B.\(80^\circ \)

C.\(40^\circ \)

D.\(20^\circ \)

Punkty \( A \), \( B \) i \( C \) leżą na okręgu o środku \( O \) (zobacz rysunek). Zaznaczony na rysunku wypukły kąt środkowy \( AOB \) ma miarę

A.\(60^\circ \)

B.\(100^\circ \)

C.\(120^\circ \)

D.\(140^\circ \)

Na okręgu o środku \( S \) leżą punkty \( A, B, C \text{ i } D \). Odcinek \( AB \) jest średnicą tego okręgu. Kąt między tą średnicą a cięciwą \( AC \) jest równy \( 21^\circ \) (zobacz rysunek).

Kąt \( \alpha \) między cięciwami \( AD \) i \( CD \) jest równy

A.\( 21^\circ \)

B.\( 42^\circ \)

C.\( 48^\circ \)

D.\( 69^\circ \)

Kąt \(ASB\) jest kątem środkowym w okręgu i jego miara wynosi \(100^\circ \). Miara zaznaczonego kąta \(\alpha \) jest równa

A.\( 40^\circ \)

B.\( 45^\circ \)

C.\( 50^\circ \)

D.\( 60^\circ \)

Miara kąta wpisanego w okrąg jest o \(20^\circ \) mniejsza od miary kąta środkowego opartego na tym samym łuku. Wynika stąd, że miara kąta wpisanego jest równa

A.\( 30^\circ \)

B.\( 20^\circ \)

C.\( 10^\circ \)

D.\( 5^\circ \)

W okręgu o środku \(O\) dany jest kąt o mierze \(50^\circ \), zaznaczony na rysunku.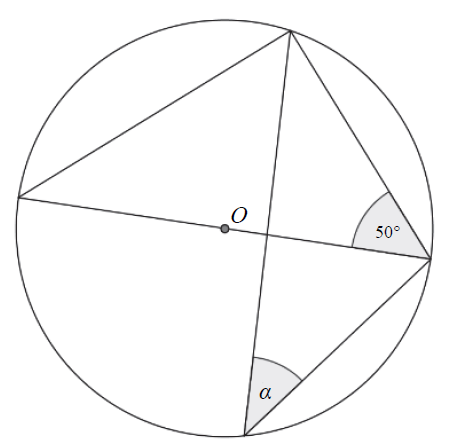

Miara kąta oznaczonego na rysunku literą \(\alpha \) jest równa

A.\( 40^\circ \)

B.\( 50^\circ \)

C.\( 20^\circ \)

D.\( 25^\circ \)

Punkty \(A\), \(B\), \(C\), \(D\) są położone w tej kolejności na okręgu o środku \(O\) (zobacz rysunek). Odcinek \(DB\) jest średnicą tego okręgu i \(|\sphericalangle BAC|=\alpha \), \(|\sphericalangle CBD|=\beta \). Wykaż, że \(\alpha +\beta =90^\circ \).