Matura podstawowa - kurs - część 38 - zadania

Drukuj

Poziom podstawowy

Cały kurs na: http://www.matemaks.pl/matematyka-matura-podstawowa-kurs.html.

W układzie współrzędnych zaznaczono kąt \(\alpha \).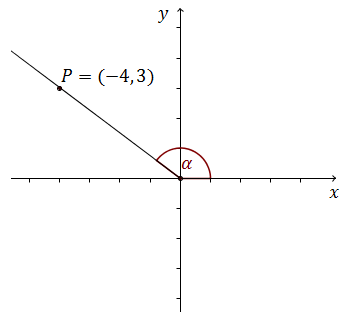

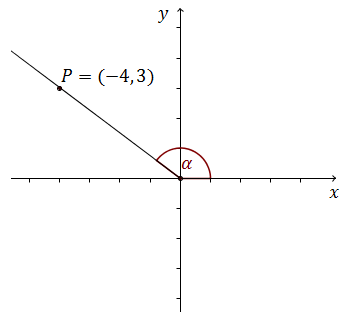Jedno z ramion kąta \(\alpha \) przechodzi przez punkt \(P=(-4,3)\). Wtedy:

A.\( \cos \alpha = \frac{4}{5} \)

B.\( \cos \alpha = -\frac{4}{5} \)

C.\( \cos \alpha = -\frac{4}{3} \)

D.\( \cos \alpha = -\frac{3}{4} \)

Kąt \(\alpha \) jest ostry i \(\sin \alpha =\frac{2}{5}\). Wówczas \(\cos \alpha \) jest równy

A.\( \frac{5}{2} \)

B.\( \frac{\sqrt{21}}{4} \)

C.\( \frac{3}{5} \)

D.\( \frac{\sqrt{21}}{5} \)

Sinus kąta ostrego \(\alpha \) jest równy \(\frac{3}{4}\). Wówczas

A.\( \cos \alpha =\frac{1}{4} \)

B.\( \cos \alpha =\frac{\sqrt{7}}{4} \)

C.\( \cos \alpha =\frac{7}{16} \)

D.\( \cos \alpha =\frac{\sqrt{13}}{16} \)

W trójkącie prostokątnym o długościach przyprostokątnych \(2\) i \(5\) cosinus większego z kątów ostrych jest równy

A.\( \frac{5}{2} \)

B.\( \frac{2}{5} \)

C.\( \frac{2}{\sqrt{29}} \)

D.\( \frac{5}{\sqrt{29}} \)

Kosinus kąta ostrego rombu jest równy \(\frac{\sqrt{3}}{2}\), bok rombu ma długość \(3\). Pole tego rombu jest równe

A.\( \frac{9}{2} \)

B.\( \frac{9\sqrt{3}}{4} \)

C.\( \frac{9\sqrt{3}}{2} \)

D.\( 6 \)

W trójkącie prostokątnym długość jednej z przyprostokątnych jest równa \(7\), zaś długość przeciwprostokątnej jest równa \(8\). Zatem tangens mniejszego kąta ostrego w tym trójkącie jest równy:

A.\( \frac{15}{7} \)

B.\( \frac{8}{15} \)

C.\( \frac{\sqrt{15}}{7} \)

D.\( \frac{7\sqrt{15}}{15} \)

Maszt telekomunikacyjny rzuca cień, który jest \(2\) razy krótszy niż wysokość masztu. Oblicz cosinus kąta, pod jakim padają promienie słoneczne.

\(\cos \alpha =\frac{\sqrt{5}}{5}\)

W trójkącie prostokątnym o bokach \(6, 8, 10\), tangens najmniejszego kąta jest równy

A.\(\frac{3}{4} \)

B.\(1\frac{1}{3} \)

C.\(\frac{3}{5} \)

D.\(\frac{4}{5} \)

W trójkącie prostokątnym najdłuższy bok ma długość \(25\), a najkrótszy \(7\). Tangens najmniejszego kąta tego trójkąta jest równy:

A.\(\frac{7}{24} \)

B.\(\frac{24}{7} \)

C.\(\frac{7}{25} \)

D.\(\frac{24}{25} \)

Liczba \( \sin 150^\circ \) jest równa liczbie

A.\( \cos 60^\circ \)

B.\( \cos 120^\circ \)

C.\( \operatorname{tg} 120^\circ \)

D.\( \operatorname{tg} 60^\circ \)

W trójkącie, przedstawionym na rysunku poniżej, sinus kąta ostrego \(\alpha \) jest równy

A.\( \frac{1}{5} \)

B.\( \frac{\sqrt{6}}{12} \)

C.\( \frac{5}{24} \)

D.\( \frac{2\sqrt{6}}{5} \)

Dany jest trójkąt prostokątny o kątach ostrych \(\alpha \) i \(\beta \), w którym \(\sin \alpha = \frac{\sqrt{6}}{3}\). Wtedy

A.\( \cos \alpha =\frac{\sqrt{3}}{2} \)

B.\( \cos \beta =\frac{\sqrt{6}}{3} \)

C.\( \operatorname{tg} \alpha =\frac{\sqrt{3}}{3} \)

D.\( \operatorname{tg} \beta =\frac{\sqrt{6}}{2} \)