Matura podstawowa - kurs - część 37 - zadania

W tym nagraniu wideo omawiam najważniejsze wiadomości dotyczące ciągu geometrycznego.

W ciągu geometrycznym \((a_n)\) mamy \(a_3 = 5\) i \(a_4 = 15\). Wtedy wyraz \(a_5\) jest równy.

Dany jest ciąg geometryczny \( (a_n) \) , w którym \( a_1=64 \) i \( q=-\frac{1}{2} \). Wówczas

Ciąg geometryczny \( (a_n) \) określony jest wzorem \( a_n=\frac{3^n}{4} \). Iloraz tego ciągu jest równy:

Ciąg geometryczny \( (a_n) \) określony jest wzorem \( a_n=-\frac{3^n}{4} \) dla \( n\ge 1 \). Iloraz tego ciągu jest równy

Dany jest ciąg geometyczny \( (a_n) \), w którym \( a_1=-\sqrt{2},\ a_2=2,\ a_3=-2\sqrt{2} \) . Dziesiąty wyraz tego ciągu, czyli \( a_{10} \), jest równy

Liczby \(64, x, 4\) są odpowiednio pierwszym, drugim i trzecim wyrazem malejącego ciągu geometrycznego. Oblicz piąty wyraz tego ciągu.

Ciąg \((27, 18, x+5)\) jest geometryczny. Wtedy

Trzeci wyraz ciągu geometrycznego równa się \(45\), a szósty wynosi \(1215\). Znajdź sumę ośmiu pierwszych wyrazów tego ciągu.

Ciąg geometryczny składa się z pięciu wyrazów, których suma wynosi \(124\). Iloraz sumy wyrazów skrajnych przez wyraz środkowy równy jest \(4{,}25\). Wyznacz ten ciąg.

Wyznacz rosnący ciąg geometryczny, wiedząc, że suma wyrazów skrajnych jest równa \(34\), iloczyn tych wyrazów \(64\), a suma wszystkich wyrazów ciągu wynosi \(62\).

Jaką jednakową liczbę należy dodać do każdej z liczb \(1, 10, 46,\) aby otrzymane sumy utworzyły ciąg geometryczny?

Liczby \(3x−4\), \(8\), \(2\) w podanej kolejności są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wtedy

Nieskończony ciąg geometryczny \((a_n)\) jest określony wzorem \(a_n=7\cdot 3^{n+1}\), dla \(n\ge 1\). Oblicz iloraz \(q\) tego ciągu.

Ciąg \( (2x – 1, y, 6x + 3)\ \) jest arytmetyczny, a ciąg \( (3, y, 27)\ \) jest geometryczny rosnący. Oblicz \(x\) i \(y\).

Liczby: \( x-2,\ 6,\ 12 \), w podanej kolejności, są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba \( x \) jest równa

W dziewięciowyrazowym ciągu geometrycznym o wyrazach dodatnich pierwszy wyraz jest równy \(3\), a ostatni wyraz jest równy \(12\). Piąty wyraz tego ciągu jest równy

Kwadrat \(K_1\) ma bok długości \(a\). Obok niego rysujemy kolejno kwadraty \(K_2, K_3, K_4,...\) takie, że kolejny kwadrat ma bok połowę mniejszy od boku poprzedniego kwadratu (zobacz rysunek). 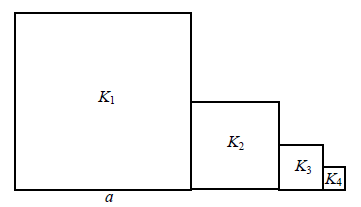Wyznacz pole kwadratu \(K_{12}\).

Dany jest ciąg geometryczny \((a_n)\), w którym pierwszy wyraz jest równy \(6\), a czwarty \(12\sqrt{2}\). Liczba \(\sqrt[3]{a_3-4}\) jest równa

Ciąg \((a_n)\) jest geometryczny oraz \(a_1=2\), \(a_2=6\). Liczby \(a_3, x, \frac{x}{2}\) w podanej kolejności tworzą ciąg arytmetyczny. Oblicz \(x\).

W rosnącym ciągu geometrycznym \((a_n)\), określonym dla \(n\ge 1\), spełniony jest warunek \(a_4=3a_1\). Iloraz \(q\) tego ciągu jest równy