Matura podstawowa - kurs - część 27 - zadania

Drukuj

Poziom podstawowy

Cały kurs na: http://www.matemaks.pl/matematyka-matura-podstawowa-kurs.html.

Na rysunku przedstawiono fragment wykresu funkcji kwadratowej \( f \).

Funkcja \( f \) określona jest wzorem

A.\(f(x)=-\frac{1}{2}(x-3)(x+1) \)

B.\(f(x)=\frac{1}{2}(x-3)(x+1) \)

C.\(f(x)=-\frac{1}{2}(x+3)(x-1) \)

D.\(f(x)=\frac{1}{2}(x+3)(x-1) \)

Parabola o wierzchołku \(W = (−3, 5)\) i ramionach skierowanych w dół może być wykresem funkcji określonej wzorem

A.\( y=2\cdot (x+3)^2+5 \)

B.\( y=-2\cdot (x-3)^2+5 \)

C.\( y=-2\cdot (x+3)^2+5 \)

D.\( y=-2\cdot (x-3)^2-5 \)

Funkcja kwadratowa, której zbiorem wartości jest przedział \( ( -\infty, -3\rangle \) , może być określona wzorem

A.\(y=(x+2)^2-3 \)

B.\(y=-(x+3)^2 \)

C.\(y=-(x-2)^2-3 \)

D.\(y=-x^2+3 \)

Funkcja kwadratowa \(y=x^2+bx+c\) jest malejąca dla \(x\in (-\infty ;2 \rangle\) a zbiorem jej wartości jest przedział \(\langle -4;\infty )\). Postać kanoniczna tej funkcji opisana jest wzorem

A.\( f(x)=(x-2)^2-4 \)

B.\( f(x)=(x+2)^2+4 \)

C.\( f(x)=(x+4)^2+2 \)

D.\( f(x)=(x-4)^2+2 \)

Wskaż funkcję kwadratową, której zbiorem wartości jest przedział \( (-\infty ;3 \rangle \).

A.\(f(x)=-(x-2)^2+3 \)

B.\(f(x)=(2-x)^2+3 \)

C.\(f(x)=-(x+2)^2-3 \)

D.\(f(x)=(2-x)^2-3 \)

Zbiorem wartości funkcji kwadratowej \(f(x)=-\frac{1}{3}x^2-2x+c\) jest przedział \((-\infty ,7\rangle \). Zatem współczynnik \(c\) jest równy

A.\( -3 \)

B.\( 4 \)

C.\( 7 \)

D.\( 10 \)

Wskaż funkcję kwadratową, której zbiorem wartości jest przedział \(\langle-2, \infty )\).

A.\( y=-2x^2+2 \)

B.\( y=-(x+1)^2-2 \)

C.\( y=2(x-1)^2+2 \)

D.\( y=(x+1)^2-2 \)

Wykresem funkcji kwadratowej \( f(x)=2x^2+bx+c \) jest parabola, której wierzchołkiem jest punkt \( W=(4,0) \). Oblicz wartości współczynników \( b \) i \( c \).

\(b=-16\), \(c=32\)

W układzie współrzędnych narysowano część paraboli o wierzchołku w punkcie \( A=(2, 4) \), która jest wykresem funkcji kwadratowej \( f \).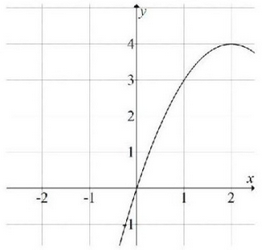

Funkcja \( f \) może być opisana wzorem

A.\(f(x)=(x-2)^2+4 \)

B.\(f(x)=(x+2)^2+4 \)

C.\(f(x)=-(x-2)^2+4 \)

D.\(f(x)=-(x+2)^2+4 \)

Funkcja kwadratowa \(f\) określona jest wzorem \(f(x) = ax^2 + bx + c\). Zbiorem rozwiązań nierówności \(f(x) \gt 0\) jest przedział \((0,12)\). Największa wartość funkcji \(f\) jest równa \(9\). Oblicz współczynniki \(a\), \(b\) i \(c\) funkcji \(f\).

\(a=-\frac{1}{4}\), \(b=3\), \(c=0\)

Wyznacz wzór funkcji kwadratowej \(f\) w postaci ogólnej, wiedząc, że zbiorem wartości tej funkcji jest przedział \((-\infty ,-1\rangle \), a wartość \(-5\) osiąga ona dla dwóch argumentów: \(2\) i \(10\).

\(f(x)=-\frac{1}{4}x^2+3x-10\)

Na rysunku są przedstawione fragmenty wykresów funkcji kwadratowych \(f\) i \(g\). Funkcja \(f\) jest określona wzorem \(f(x)=-x^2+6x-5\), a mniejsze z jej miejsc zerowych jest jednocześnie miejscem zerowym funkcji \(g\). Wierzchołek \(W\) paraboli, która jest wykresem funkcji \(f\), leży na wykresie funkcji \(g\), a wierzchołek \(Z\) paraboli będącej wykresem funkcji \(g\) leży na osi \(Oy\) układu współrzędnych. Wyznacz wzór funkcji \(g\).

\(g(x)=\frac{1}{2}(x-1)(x+1)\)