Matura podstawowa - kurs - część 21 - zadania
Poziom podstawowy
Cały kurs na: http://www.matemaks.pl/matematyka-matura-podstawowa-kurs.html.Zbiorem wartości funkcji przedstawionej na rysunku jest przedział 
A.\(\langle -3,6 \rangle\)
B.\(\langle -1,4 \rangle\)
C.\((1,3)\)
D.\((-2,2)\)
Zbiorem wartości funkcji, której wykres przedstawiono na rysunku jest przedział:
A.\( \langle -4,5 \rangle \)
B.\( \langle -3,4 \rangle \)
C.\( \langle -2,4 \rangle \)
D.\( \langle -3,2 \rangle \)
Na rysunku przedstawiony jest wykres funkcji \(y = f(x)\). 
Zbiorem wartości tej funkcji jest
Zbiorem wartości tej funkcji jest A.\( \langle -4,3 \rangle \)
B.\( \langle -4,-1 \rangle \cup \langle 1,3 \rangle\)
C.\( \langle -4,-1 \rangle \cup ( 1,3 \rangle \)
D.\( \langle -5,6 \rangle \)
Na rysunku przedstawiony jest wykres funkcji \(y=f(x)\). 
Które równanie ma dokładnie trzy rozwiązania?
Które równanie ma dokładnie trzy rozwiązania? A.\( f(x)=0 \)
B.\( f(x)=1 \)
C.\( f(x)=2 \)
D.\( f(x)=3 \)
Na rysunku przedstawiono wykres funkcji \(f\). 
Odczytaj z wykresu i zapisz:
Odczytaj z wykresu i zapisz: - zbiór wartości funkcji \(f\),
- przedział maksymalnej długości, w którym \(f\) jest malejąca.
Na rysunku przedstawiony jest wykres funkcji \(f(x)\) określonej dla \(x\in [-7, 8]\). 
Odczytaj z wykresu i zapisz:
a) największą wartość funkcji \(f\),
b) zbiór rozwiązań nierówności \(f(x)\lt 0\).
Odczytaj z wykresu i zapisz:a) największą wartość funkcji \(f\),
b) zbiór rozwiązań nierówności \(f(x)\lt 0\).
Na rysunku przedstawiono wykres funkcji \(y=f(x)\). 
Największa wartość funkcji \(f\) w przedziale \([-1,1]\) jest równa
Największa wartość funkcji \(f\) w przedziale \([-1,1]\) jest równa A.\( 4 \)
B.\( 3 \)
C.\( 2 \)
D.\( 1 \)
Zbiorem wartości funkcji \(f\) jest przedział 
A.\( \langle -3,5 \rangle \)
B.\( \langle -6,7 \rangle \)
C.\( \langle 0,6 \rangle \)
D.\( \langle -5,8 \rangle \)
Przedziałem, w którym funkcja \(f\) przyjmuje tylko wartości ujemne, jest
A.\( \langle 5,0 \rangle \)
B.\( ( 5,7 \rangle \)
C.\( \langle 0,7 \rangle \)
D.\( \langle -6,5 \rangle \)
Rysunek przedstawia wykres pewnej funkcji \( y=f(x) \), określonej dla \( x \in \langle -4,4 \rangle \). 
Zbiór wszystkich argumentów, dla których funkcja \( f \) przyjmuje wartości niedodatnie, to zbiór
Zbiór wszystkich argumentów, dla których funkcja \( f \) przyjmuje wartości niedodatnie, to zbiór A.\(\langle 0,3 )\cup ( 3,4 \rangle \)
B.\(\langle -4,-3 \rangle\cup \langle 0,4 \rangle \)
C.\((-4,-3)\cup (0,3)\cup (3,4) \)
D.\((-2,1)\cup (3,4) \)
Największą wartością funkcji \( f \) jest 
A.\(3 \)
B.\(0 \)
C.\(-3 \)
D.\(8 \)
Na rysunku przedstawiono wykres funkcji \(f\).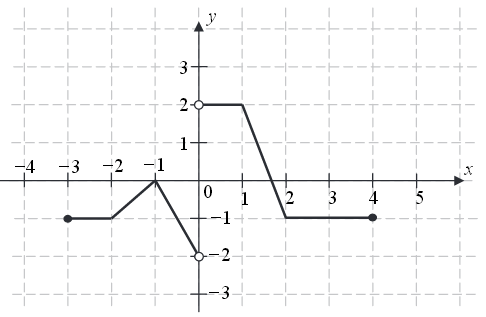 
Zbiorem wartości funkcji \(f\) jest
Zbiorem wartości funkcji \(f\) jest A.\( (-2,2\rangle \)
B.\( \langle -2,2\rangle \)
C.\( \langle -2,2) \)
D.\( (-2,2) \)
Tematy nadrzędne