Matura podstawowa - kurs - część 13 - zadania

Najmniejszą liczbą całkowitą spełniającą nierówność \(\frac{x}{5}+\sqrt{7}\gt 0\) jest

Wskaż największą liczbę całkowitą spełniającą nierówność \(\frac{x}{4}-\sqrt{3}\lt 0\).

Wskaż rysunek, na którym przedstawiony jest zbiór rozwiązań nierówności \(2(3 − x) > x\).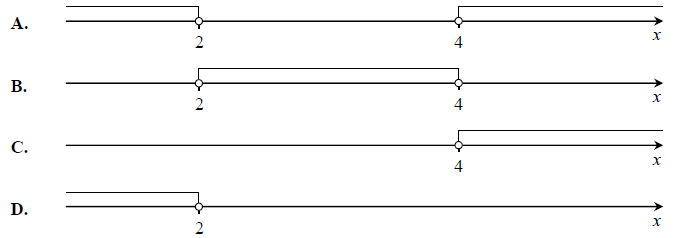

Zbiorem rozwiązań nierówności \(ax+4\ge 0\) z niewiadomą \(x\) jest przedział \((-\infty ,2 \rangle\). Wyznacz \(a\).

Najmniejszą liczbą całkowitą spełniającą nierówność \(2(x − 2) \le 4(x −1)+1\) jest

Zbiorem wszystkich rozwiązań nierówności \(x\sqrt{3}+4\ge 2x+\sqrt{12}\) jest przedział

Największą liczbą całkowitą spełniającą nierówność \((4 + x)^2 \lt (x - 4)(x + 4)\) jest

Najmniejszą liczbą całkowitą należącą do zbioru rozwiązań nierówności \(\frac{3}{8}+\frac{x}{6}\lt \frac{5x}{12}\) jest

Wskaż przedział, który jest zbiorem rozwiązań nierówności \(\frac{x}{4}+\frac{1}{6}\lt \frac{x}{3}\)

Najmniejszą liczbą całkowitą spełniającą nierówność \(\frac{x}{2}\le \frac{2x}{3}+\frac{1}{4}\) jest

Zbiorem rozwiązań nierówności \(\frac{2-x}{3}-\frac{2x-1}{2} \lt x \) jest przedział

Ile liczb całkowitych \(x\) spełnia nierówność \(\frac{2}{7}\lt \frac{x}{14}\lt \frac{4}{3}\)?

Zbiór wszystkich liczb rzeczywistych spełniających nierówność \(\frac{3}{5}-\frac{2x}{3}\ge \frac{x}{6}\) jest przedziałem