Matura podstawowa - kurs - część 12 - zadania

Drukuj

Poziom podstawowy

Na filmie pokazuję praktyczną metodę na szybkie rysowanie dokładnych wykresów funkcji liniowych.

Czas nagrania: 13 min.

Na jednym z poniższych rysunków przedstawiono interpretację geometryczną układu równań \[\begin{cases} x+3y=-5 \\ 3x-2y=-4 \end{cases} \] Wskaż ten rysunek.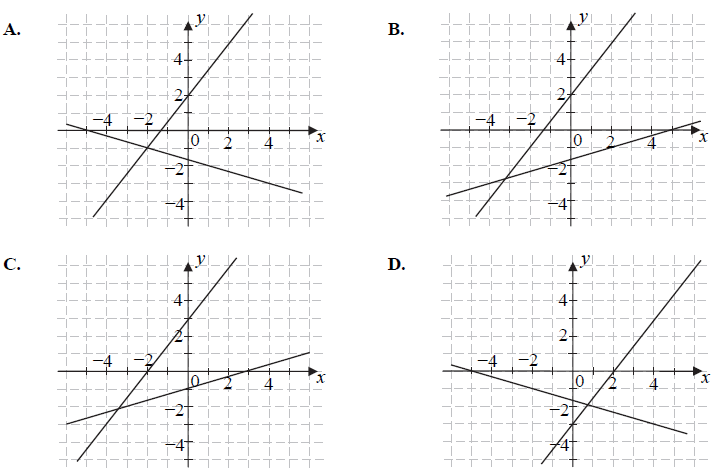

Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.

Wskaż ten układ.

A.\(\begin{cases} {y=x-1}\\ {y=-2x+4} \end{cases} \)

B.\(\begin{cases} {y=x-1}\\ {y=2x+4} \end{cases} \)

C.\(\begin{cases} {y=x+1}\\ {y=-2x+4} \end{cases} \)

D.\(\begin{cases} {y=x+1}\\ {y=2x+4} \end{cases} \)

Interpretację geometryczną układu równań \[\begin{cases} x-y=2\\ -2x+2y=4 \end{cases} \] przedstawiono na rysunku: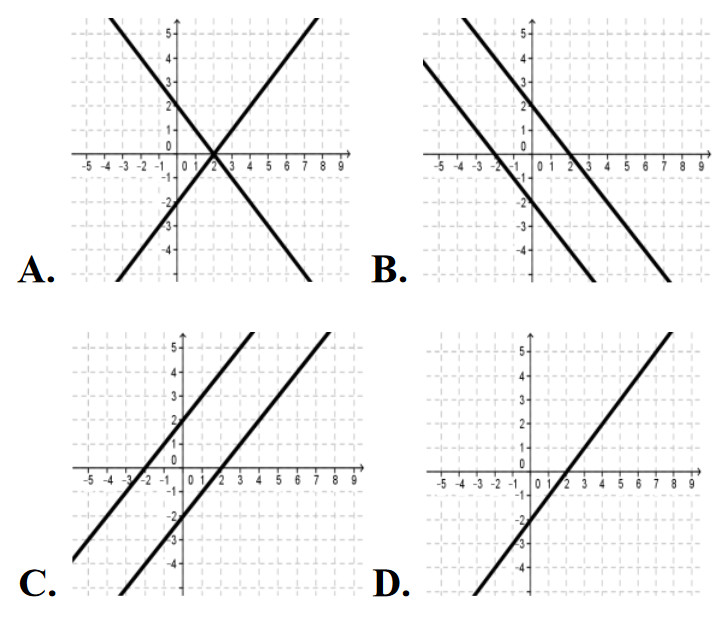

Układ równań \(\begin{cases} y=3x+2 \\ y=(m-2)x+5 \end{cases} \) nie ma rozwiązań, gdy

A.\( m=2 \)

B.\( m=3 \)

C.\( m=4 \)

D.\( m=5 \)

Układ równań \(\begin{cases} x-y=3 \\ 2x+0{,}5y=4 \end{cases} \) opisuje w układzie współrzędnych na płaszczyźnie

A.zbiór nieskończony.

B.dokładnie 2 różne punkty.

C.dokładnie jeden punkt.

D.zbiór pusty.

Rozwiąż układ równań \(\begin{cases} x+3y=5\\ 2x-y=3 \end{cases} \).

\(\begin{cases} x=2 \\ y=1 \end{cases} \)

Układ równań \(\begin{cases} 4x+2y=10\\ 6x+ay=15 \end{cases} \) ma nieskończenie wiele rozwiązań, jeśli

A.\( a=-1 \)

B.\( a=0 \)

C.\( a=2 \)

D.\( a=3 \)

Rozwiązaniem układu równań \(\begin{cases} 3x-5y=0\\ 2x-y=14 \end{cases} \) jest para liczb \((x,y)\) takich, że

A.\(x\lt 0\)i\(y\lt 0\)

B.\(x\lt 0\)i\(y>0\)

C.\(x>0\)i\(y\lt 0\)

D.\(x>0\)i\(y>0\)