Matura 2024 grudzień PR

Drukuj

Poziom rozszerzony

Pliki do pobrania:
Arkusz Karta odpowiedzi
Rozwiązania wideo są w trakcie przygotowania.

Ładunek elektryczny zgromadzony w kondensatorze można opisać zależnością \[ Q(t)=Q_{0} \cdot \beta^{-t} \quad \text { dla } \quad t \geq 0 \] gdzie:
\(Q_{0}\) - ładunek elektryczny zgromadzony w kondensatorze w chwili początkowej \((t=0)\) wyrażony w milikulombach
\(Q\) - ładunek elektryczny zgromadzony w kondensatorze w chwili \(t\) (licząc od chwili początkowej) wyrażony w milikulombach
\(\beta\) - stała dodatnia
\(t\) - czas wyrażony w sekundach.

Wiadomo, że w chwili \(t=4 \mathrm{~s}\) w kondensatorze był zgromadzony ładunek \(2\) milikulombów, a w chwili \(t=6 \mathrm{~s}\) - ładunek \(18\) milikulombów.

Oblicz, ile milikulombów ładunku było zgromadzone w tym kondensatorze w chwili \(t=5 \mathrm{~s}\). Zapisz obliczenia.

\(6\) milikulombów.

Okrąg \(\mathcal{O}\) jest styczny do boków \(A C\) i \(B C\) trójkąta \(A B C\) oraz przecina bok \(A B\) tego trójkąta w punktach \(M\) oraz \(N\), przy czym \(0\lt |A M|\lt |A N|\lt |A B|\).

Wykaż, że jeśli \(|A M|=|B N|\), to trójkąt \(A B C\) jest równoramienny.

Iloczyn długości średnicy podstawy walca i wysokości walca jest równy \(12 \sqrt{3}\).
Pole powierzchni całkowitej tego walca jest równe \(12 \pi(\sqrt{3}+1)\).

Oblicz objętość tego walca. Zapisz obliczenia.

\(V=18\pi \sqrt{2}\)

Wykaż, że \[ \frac{1}{\log _{2} 35+1}+\frac{1}{\log _{7} 140-\log _{7} 2}+\frac{1}{\log _{5} 7+\log _{5} 2+1}=1 \]

W pewnej lokalnej społeczności \(35 \%\) osób ma wyższe wykształcenie. W tej społeczności językiem niemieckim dobrze włada \(70 \%\) osób mających wyższe wykształcenie i \(40 \%\) osób bez wyższego wykształcenia.
Spośród członków tej społeczności wybieramy losowo jedną osobę.

Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wybierzemy osobę z wyższym wykształceniem, jeżeli wiadomo, że ta osoba dobrze włada językiem niemieckim. Wynik zapisz w postaci ułamka dziesiętnego w zaokrągleniu do części setnych. Zapisz obliczenia.

\(P(B1|A)\simeq 0,49\)

Rozwiąż równanie \[ |4x-8|+|x-2|=|2-x|+|x+2|+4 \]

\(x=\frac{2}{5}\) lub \(x=\frac{14}{3}\)

W kartezjańskim układzie współrzędnych \((x, y)\) dane są:
okrąg o równaniu \((x+1)^{2}+(y-3)^{2}=50\) i punkty \(A=(6,4)\) oraz \(B=(-6,8)\).
Punkt \(C\) leży na tym okręgu i \(|A C|=|B C|\).

Oblicz współrzędne punktu \(C\). Rozważ wszystkie przypadki. Zapisz obliczenia.

\(C=(\sqrt{5}-1,3 \sqrt{5}+3)\) lub \(C=(-\sqrt{5}-1,-3 \sqrt{5}+3)\)

Oblicz granicę \[ \lim _{n \rightarrow+\infty} \frac{1+3+5+7+\ldots+(2 n+1)}{\binom{n}{2}} \] gdzie \(1+3+5+7+\ldots+(2 n+1)\) jest sumą kolejnych liczb naturalnych nieparzystych.

\(2\)

Rozwiąż równanie \[ \sin ^{4} x=\sin x \cdot \cos x-\cos ^{4} x \] w zbiorze \([-\pi, 2 \pi]\). Zapisz obliczenia.

\(\left(-\frac{3}{4} \pi\right), \frac{1}{4} \pi\) oraz \(\frac{5}{4} \pi\)

Trzeci i piąty wyraz malejącego ciągu arytmetycznego \((a_{n})\), określonego dla każdej liczby naturalnej \(n \geq 1\), spełniają warunek \(a_{3}+a_{5}=10\).
Trzywyrazowy ciąg ( \(2 a_{1}+4, a_{4}-1,-\frac{1}{8} a_{7}\) ) jest geometryczny.

Oblicz wyrazy tego ciągu geometrycznego. Zapisz obliczenia.

\(\left(32,4,\frac{1}{2}\right)\)

Funkcja kwadratowa \(f\) zmiennej rzeczywistej \(x\) jest określona wzorem \[ f(x)=x^{2}-3 x-m^{2}+m+3 \]

Wyznacz wszystkie wartości parametru \(m\), dla których funkcja \(f\) ma dwa różne miejsca zerowe \(x_{1}, x_{2}\) spełniające warunek \(\left|x_{1}^{2}-x_{2}^{2}\right| \leq 12\). Zapisz obliczenia.

\(m \in\left[\frac{1-2 \sqrt{5}}{2},-\frac{1}{2}\right) \cup\left(\frac{3}{2}, \frac{1+2 \sqrt{5}}{2}\right]\)

W trójkącie ostrokątnym \(ABC\) miara kąta \(BAC\) jest dwa razy większa od miary kąta \(ABC\). Punkt \(D\) jest środkiem boku \(AB\). Niech \(\alpha\) oznacza miarę kąta \(ABC\), natomiast \(\beta\)-miarę kąta \(ADC\) (zobacz rysunek).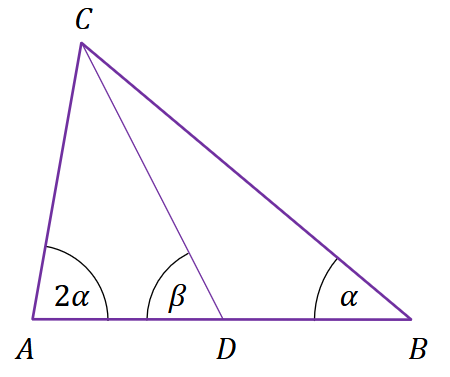

Oblicz \(\frac{\operatorname{tg} \beta}{\sin (2 \alpha)}\). Zapisz obliczenia.

\(\frac{\operatorname{tg} \beta}{\sin (2 \alpha)}=2\)

Funkcja \(f\) jest określona wzorem \(f(x)=\frac{12 x-84}{x-8}\) dla każdego \(x \in(-\infty, 8)\). W kartezjańskim układzie współrzędnych \((x, y)\) rozważamy wszystkie czworokąty \(O B C D\), w których: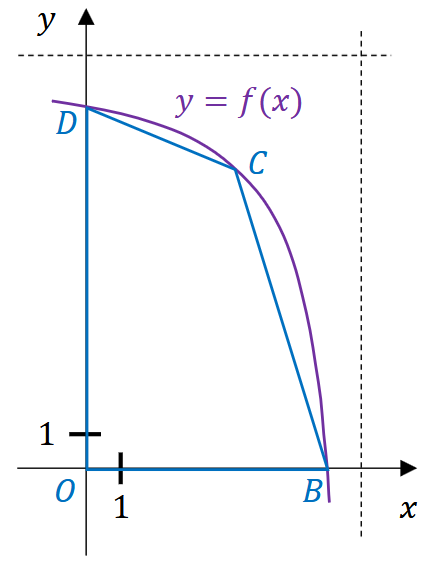

wierzchołek \(O\) ma współrzędne \((0,0)\)
wierzchołki \(B\) oraz \(D\) są punktami przecięcia wykresu funkcji \(f\) z osią odpowiednio - \(Ox\) i \(Oy\)
wierzchołek \(C\) ma obie współrzędne dodatnie i leży na wykresie funkcji \(f\) (zobacz rysunek).

(zobacz rysunek).

Wykaż, że pole \(P\) czworokąta \(OBCD\) w zależności od pierwszej współrzędnej \(x\) punktu \(C\) jest określone wzorem \[ P(x)=\frac{21}{4} \cdot \frac{x^{2}-56}{x-8} \]

Pole \(P\) czworokąta \(OBCD\) w zależności od pierwszej współrzędnej \(x\) punktu \(C\) jest określone wzorem \[ P(x)=\frac{21}{4} \cdot \frac{x^{2}-56}{x-8} \] dla \(x \in(0,7)\).

Oblicz współrzędne wierzchołka \(C\), dla których pole czworokąta \(O B C D\) jest największe. Zapisz obliczenia.

\(C=(8-2\sqrt{2},12-3\sqrt{2})\)