Matura rozszerzona 2024 - czerwiec - termin dodatkowy
Poziom rozszerzony
W chwili początkowej \((t=0)\) zainicjowano pewną reakcję chemiczną, w której brał udział związek A.
W wyniku tej reakcji masa \(m\) związku A zmieniała się w czasie zgodnie z zależnością \[ m(t)=a \cdot 2^{-0,05 \cdot t}+b \quad \text { dla } \quad t \geq 0 \] gdzie:
\(m\) - masa związku A wyrażona w gramach,
\(t\) - czas wyrażony w sekundach (liczony od chwili \(t=0\) ),
\(a, b\) - współczynniki liczbowe.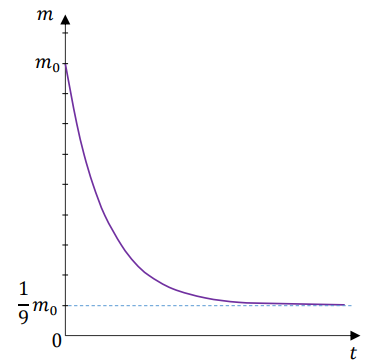
W wyniku tej reakcji masa \(m\) związku A zmieniała się w czasie zgodnie z zależnością \[ m(t)=a \cdot 2^{-0,05 \cdot t}+b \quad \text { dla } \quad t \geq 0 \] gdzie:
\(m\) - masa związku A wyrażona w gramach,
\(t\) - czas wyrażony w sekundach (liczony od chwili \(t=0\) ),
\(a, b\) - współczynniki liczbowe.
Masa początkowa związku A (tj. masa w chwili \(t=0\) ) była równa \(m_{0}\) gramów.
Po osiągnięciu stanu równowagi (tj. gdy \(t \rightarrow \infty\) ) masa tego związku była równa \(\frac{1}{9}\) jego masy początkowej (zobacz rysunek).
Po osiągnięciu stanu równowagi (tj. gdy \(t \rightarrow \infty\) ) masa tego związku była równa \(\frac{1}{9}\) jego masy początkowej (zobacz rysunek).

Oblicz, po ilu sekundach (licząc od chwili zainicjowania tej reakcji) przereagowało \(87,5 \%\) masy początkowej tego związku. Zapisz obliczenia.
Oblicz granicę \[ \lim _{x \rightarrow 3^{-}} \frac{|x-3|}{x^{2}-9} \] Zapisz obliczenia.
Funkcja \(f\) jest określona wzorem \(f(x)=\frac{2 x+1}{x-4}\) dla każdej liczby rzeczywistej \(x \neq 4\).
W kartezjańskim układzie współrzędnych \((x, y)\) punkt \(P=(x_{0}, 5)\) należy do wykresu funkcji \(f\).
W kartezjańskim układzie współrzędnych \((x, y)\) punkt \(P=(x_{0}, 5)\) należy do wykresu funkcji \(f\).
Oblicz \(x_{0}\) oraz wyznacz równanie stycznej do wykresu funkcji \(f\) w punkcie \(P\). Zapisz obliczenia.
Doświadczenie losowe polega na dziesięciokrotnym rzucie symetryczną monetą.
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w tym doświadczeniu losowym orzeł wypadł dokładnie trzy razy z rzędu, jeśli wiadomo, że wypadł dokładnie trzy razy. Zapisz obliczenia.
Wykaż, że dla każdej liczby dodatniej \(a\) i każdej liczby dodatniej \(b\) takich, że \(a+b=1\), prawdziwa jest nierówność \[ \frac{1}{2 a+b}+\frac{1}{a+2 b} \geq \frac{4}{3} \]
Długości podstaw trapezu równoramiennego są równe \(a\) oraz \(b\), przy czym \(a\gt b\). W ten trapez można wpisać okrąg.
Wykaż, że pole tego trapezu jest większe od \(a \cdot b\).
Nieskończony ciąg geometryczny \((a_{n})\) jest określony dla każdej liczby naturalnej \(n \geq 1\). Suma wszystkich wyrazów ciągu \((a_{n})\) o numerach nieparzystych jest równa \(16\), tj. \[ a_{1}+a_{3}+a_{5}+\ldots=16 \] Ponadto \(a_{1}+a_{3}=\frac{5}{2} \cdot a_{2}\).
Wyznacz wzór ogólny na \(n\)-ty wyraz ciągu \((a_{n})\). Zapisz obliczenia.
W okrąg o promieniu \(4\) wpisano trójkąt \(ABC\). Długość boku \(AB\) jest równa \(6\). Bok \(BC\) ma długość \(4 \sqrt{3}\) i jest najdłuższym bokiem tego trójkąta.
Oblicz długość boku \(A C\) trójkąta \(A B C\). Zapisz obliczenia.
Rozwiąż równanie \[ \sin (6 x)+\sqrt{3} \cdot \sin (5 x)+\sin (4 x)=0 \] Zapisz obliczenia.
Długość krawędzi podstawy graniastosłupa prawidłowego trójkątnego jest równa \(a\).
Sinus kąta między przekątnymi ścian bocznych wychodzącymi z jednego wierzchołka graniastosłupa jest równy \(\frac{\sqrt{11}}{6}\).
Sinus kąta między przekątnymi ścian bocznych wychodzącymi z jednego wierzchołka graniastosłupa jest równy \(\frac{\sqrt{11}}{6}\).
Wyznacz pole powierzchni całkowitej tego graniastosłupa. Zapisz obliczenia.
W kartezjańskim układzie współrzędnych \((x, y)\) prosta o równaniu \(3 x+y+2=0\) przecina parabolę o równaniu \(y=x^{2}-2 x-8\) w punktach \(A\) oraz \(B\), które są kolejnymi wierzchołkami równoległoboku \(A B C D\).
Wierzchołek \(A\) ma pierwszą współrzędną ujemną.
Wierzchołek \(C\) leży na prostej o równaniu \(y=-\frac{1}{2} x+1\) i ma pierwszą współrzędną dodatnią.
Odległość punktu \(C\) od prostej zawierającej bok \(A B\) równoległoboku jest równa \(\frac{9 \sqrt{10}}{5}\).
Wierzchołek \(A\) ma pierwszą współrzędną ujemną.
Wierzchołek \(C\) leży na prostej o równaniu \(y=-\frac{1}{2} x+1\) i ma pierwszą współrzędną dodatnią.
Odległość punktu \(C\) od prostej zawierającej bok \(A B\) równoległoboku jest równa \(\frac{9 \sqrt{10}}{5}\).
Oblicz długość boku \(B C\) tego równoległoboku. Zapisz obliczenia.
Wyznacz wszystkie wartości parametru \(m\), dla których równanie \[ (3-m) \cdot x^{2}+(m+1) \cdot x-(m+1)^{2}=0 \] ma dwa różne rozwiązania rzeczywiste \(x_{1}, x_{2}\) spełniające warunek \[ x_{1}^{2}+x_{2}^{2}=x_{1} \cdot x_{2}+7 \] Zapisz obliczenia.
Rozważamy wszystkie ostrosłupy prawidłowe trójkątne, w których suma wysokości \(H\) ostrosłupa oraz promienia \(R\) okręgu opisanego na podstawie tego ostrosłupa jest równa \(6\).
Wykaż, że objętość \(V\) każdego z takich ostrosłupów w zależności od długości \(R\) promienia okręgu opisanego na podstawie ostrosłupa jest określona wzorem \[ V(R)=\frac{\sqrt{3}}{4} \cdot(6 R^{2}-R^{3}) \]
Objętość \(V\) ostrosłupa w zależności od długości \(R\) promienia okręgu opisanego na podstawie ostrosłupa jest określona wzorem \[ V(R)=\frac{\sqrt{3}}{4} \cdot(6 R^{2}-R^{3}) \] dla \(R \in(0,6)\).
Wyznacz długość promienia okręgu opisanego na podstawie tego z rozważanych ostrosłupów, którego objętość jest największa. Oblicz tę największą objętość. Zapisz obliczenia.
Tematy nadrzędne i sąsiednie