Matura 2015 maj

Drukuj

Poziom podstawowy

Szybka nawigacja do zadania numer: 5 10 15 20 25 30 .

Wskaż rysunek na którym przedstawiono przedział, będący zbiorem wszystkich rozwiązań nierówności \(-4\le x-1\le 4\).

C (na filmiku D)

Dane są liczby \(a=-\frac{1}{27}\), \(b=\log_{\frac{1}{4}}64\), \(c=\log_{\frac{1}{3}}27\). Iloczyn \(abc\) jest równy

A.\( 3 \)

B.\( \frac{1}{3} \)

C.\( -\frac{1}{3} \)

D.\( -9 \)

Kwotę \(1000\) zł ulokowano w banku na roczną lokatę oprocentowaną w wysokości \(4\%\) w stosunku rocznym. Po zakończeniu lokaty od naliczonych odsetek odprowadzany jest podatek w wysokości \(19\%\). Maksymalna kwota, jaką po upływie roku będzie można wypłacić z banku, jest równa

A.\( 1000\cdot \left ( 1+\frac{81}{100}\cdot \frac{4}{100} \right ) \)

B.\( 1000\cdot \left ( 1-\frac{19}{100}\cdot \frac{4}{100} \right ) \)

C.\( 1000\cdot \left ( 1-\frac{81}{100}\cdot \frac{4}{100} \right ) \)

D.\( 1000\cdot \left ( 1+\frac{19}{100}\cdot \frac{4}{100} \right ) \)

Równość \(\frac{m}{5-\sqrt{5}}=\frac{5+\sqrt{5}}{5}\) zachodzi dla

A.\( m=-5 \)

B.\( m=1 \)

C.\( m=4 \)

D.\( m=5 \)

Układ równań \(\begin{cases} x-y=3 \\ 2x+0{,}5y=4 \end{cases} \) opisuje w układzie współrzędnych na płaszczyźnie

A.zbiór nieskończony.

B.dokładnie 2 różne punkty.

C.dokładnie jeden punkt.

D.zbiór pusty.

Suma wszystkich pierwiastków równania \((x+3)(x+7)(x-11)=0\) jest równa

A.\( 21 \)

B.\( -1 \)

C.\( -21 \)

D.\( 1 \)

Równanie \(\frac{x-1}{x+1}=x-1\)

A.ma dokładnie dwa rozwiązania \( x=0 \), \(x=1\)

B.ma dokładnie jedno rozwiązanie \( x=-1 \)

C.ma dokładnie jedno rozwiązanie \( x=0 \)

D.ma dokładnie jedno rozwiązanie \( x=1 \)

Na rysunku przedstawiono wykres funkcji \(f\).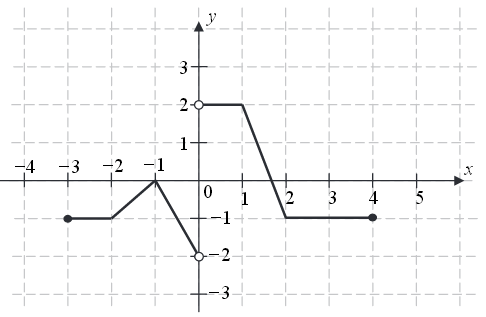

Zbiorem wartości funkcji \(f\) jest

A.\( (-2,2\rangle \)

B.\( \langle -2,2\rangle \)

C.\( \langle -2,2) \)

D.\( (-2,2) \)

Na wykresie funkcji liniowej określonej wzorem \(f(x)=(m-1)x+3\) leży punkt \(S=(5,-2)\). Zatem

A.\( m=1 \)

B.\( m=2 \)

C.\( m=-1 \)

D.\( m=0 \)

Funkcja liniowa \(f\) określona wzorem \(f(x)=2x+b\) ma takie samo miejsce zerowe, jakie ma funkcja \(g(x)=-3x+4\). Stąd wynika, że

A.\( b=-\frac{8}{3} \)

B.\( b=\frac{4}{3} \)

C.\( b=4 \)

D.\( b=-\frac{3}{2} \)

Funkcja kwadratowa określona jest wzorem \(f(x)=x^2+x+c\). Jeśli \(f(3)=4\), to

A.\( f(1)=18 \)

B.\( f(1)=6 \)

C.\( f(1)=0 \)

D.\( f(1)=-6 \)

Ile liczb całkowitych \(x\) spełnia nierówność \(\frac{2}{7}\lt \frac{x}{14}\lt \frac{4}{3}\)?

A.\( 17 \)

B.\( 16 \)

C.\( 15 \)

D.\( 14 \)

W rosnącym ciągu geometrycznym \((a_n)\), określonym dla \(n\ge 1\), spełniony jest warunek \(a_4=3a_1\). Iloraz \(q\) tego ciągu jest równy

A.\( q=\frac{1}{\sqrt[3]{3}} \)

B.\( q=\frac{1}{3} \)

C.\( q=3 \)

D.\( q=\sqrt[3]{3} \)

W układzie współrzędnych zaznaczono punkt \(P=(-4,5)\). Tangens kąta \(\alpha \) zaznaczonego na rysunku jest równy

A.\( -\frac{5}{4} \)

B.\( -1 \)

C.\( -\frac{4}{5} \)

D.\( -\frac{\sqrt{3}}{3} \)

Jeżeli \(0^\circ \lt \alpha \lt 90^\circ \) oraz \(\operatorname{tg} \alpha =2\sin \alpha \), to

A.\( \cos \alpha =\frac{\sqrt{2}}{2} \)

B.\( \cos \alpha =\frac{1}{2} \)

C.\( \cos \alpha =1 \)

D.\( \cos \alpha =\frac{\sqrt{3}}{2} \)

Miara kąta wpisanego w okrąg jest o \(20^\circ \) mniejsza od miary kąta środkowego opartego na tym samym łuku. Wynika stąd, że miara kąta wpisanego jest równa

A.\( 30^\circ \)

B.\( 20^\circ \)

C.\( 10^\circ \)

D.\( 5^\circ \)

Pole rombu o obwodzie \(8\) jest równe \(1\). Kąt ostry tego rombu ma miarę \(\alpha \). Wtedy

A.\( 29^\circ \lt \alpha \lt 30^\circ \)

B.\( 14^\circ \lt \alpha \lt 15^\circ \)

C.\( 75^\circ \lt \alpha \lt 76^\circ \)

D.\( 60^\circ \lt \alpha \lt 61^\circ \)

Prosta \(l\) o równaniu \(y=m^2x+3\) jest równoległa do prostej \(k\) o równaniu \(y=(4m-4)x-3\). Zatem:

A.\( m=2 \)

B.\( m=-2 \)

C.\( m=-2-2\sqrt{2} \)

D.\( m=2+2\sqrt{2} \)

Proste o równaniach: \(y=2mx-m^2-1\) oraz \(y=4m^2x+m^2+1\) są prostopadłe dla

A.\( m=-\frac{1}{2} \)

B.\( m=\frac{1}{2} \)

C.\( m=1 \)

D.\( m=2 \)

Dane są punkty \(M=(-2,1)\) i \(N=(-1,3)\). Punkt \(K\) jest środkiem odcinka \(MN\). Obrazem punktu \(K\) w symetrii względem początku układu współrzędnych jest punkt

A.\( K'=\left ( 2,-\frac{3}{2} \right ) \)

B.\( K'=\left ( 2,\frac{3}{2} \right ) \)

C.\( K'=\left ( \frac{3}{2},2 \right ) \)

D.\( K'=\left ( \frac{3}{2},-2 \right ) \)

W graniastosłupie prawidłowym czworokątnym \(EFGHIJKL\) wierzchołki \(E, G, L\) połączono odcinkami (tak jak na rysunku).

Wskaż kąt między wysokością \(OL\) trójkąta \(EGL\) i płaszczyzną podstawy tego graniastosłupa.

A.\( \sphericalangle OGL \)

B.\( \sphericalangle HOL \)

C.\( \sphericalangle HLO \)

D.\( \sphericalangle OHL \)

Przekrojem osiowym stożka jest trójkąt równoboczny o boku długości \(6\). Objętość tego stożka jest równa

A.\( 6\pi \)

B.\( 18\pi \)

C.\( 9\pi\sqrt{3} \)

D.\( 27\pi\sqrt{3} \)

Każda krawędź graniastosłupa prawidłowego trójkątnego ma długość równą \(8\). Pole powierzchni całkowitej tego graniastosłupa jest równe

A.\( 8^2\left ( \frac{\sqrt{3}}{2}+3 \right ) \)

B.\( \frac{8^2\sqrt{6}}{3} \)

C.\( 8^2\cdot \sqrt{3} \)

D.\( \frac{8^2}{3}\left ( \frac{\sqrt{3}}{2}+3 \right ) \)

Średnia arytmetyczna zestawu danych: \[2,4,7,8,9\] jest taka sama jak średnia arytmetyczna zestawu danych: \[2,4,7,8,9,x.\] Wynika stąd, że

A.\( x=3 \)

B.\( x=5 \)

C.\( x=6 \)

D.\( x=0 \)

W każdym z trzech pojemników znajduje się para kul, z których jedna jest czerwona, a druga - niebieska. Z każdego pojemnika losujemy jedną kulę. Niech \(p\) oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie z trzech wylosowanych kul będą czerwone. Wtedy

A.\( p=\frac{3}{8} \)

B.\( p=\frac{1}{4} \)

C.\( p=\frac{2}{3} \)

D.\( p=\frac{1}{2} \)

Rozwiąż nierówność \(2x^2-4x\gt (x+3)(x-2)\).

\(x\in (-\infty ;2)\cup (3;+\infty )\)

Wykaż, że dla każdej liczby rzeczywistej \(x\) i dla każdej liczby rzeczywistej \(y\) prawdziwa jest nierówność \(4x^2-8xy+5y^2\ge 0\).

Dany jest kwadrat \(ABCD\). Przekątne \(AC\) i \(BD\) przecinają się w punkcie \(E\). Punkty \(K\) i \(M\) są środkami odcinków - odpowiednio \(AE\) i \(EC\). Punkty \(L\) i \(N\) leżą na przekątnej \(BD\) tak, że \(|BL|=\frac{1}{3}|BE|\) i \(|DN|=\frac{1}{3}|DE|\) (zobacz rysunek). Wykaż, że stosunek pola czworokąta \(KLMN\) do pola kwadratu \(ABCD\) jest równy \(1:3\).

Oblicz najmniejszą i największą wartość funkcji kwadratowej \(f(x)=x^2-6x+3\) w przedziale \(\langle 0,4\rangle \).

\(f_{max}=3\) oraz \(f_{min}=-6\)

W układzie współrzędnych dane są punkty \(A=(-43,-12)\), \(B=(50,19)\). Prosta \(AB\) przecina oś \(Ox\) w punkcie \(P\). Oblicz pierwszą współrzędną punktu \(P\).

\(x=-7\)

Jeżeli do licznika i do mianownik nieskracalnego dodatniego ułamka dodamy połowę jego licznika, to otrzymamy \(\frac{4}{7}\), a jeżeli do licznika i do mianownika dodamy \(1\), to otrzymamy \(\frac{1}{2}\). Wyznacz ten ułamek.

\(\frac{8}{17}\)

Wysokość graniastosłupa prawidłowego czworokątnego jest równa \(16\). Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem, którego cosinus jest równy \(\frac{3}{5}\). Oblicz pole powierzchni całkowitej tego graniastosłupa.

\(P=144+384\sqrt{2}\)

Wśród \(115\) osób przeprowadzono badania ankietowe, związane z zakupami w pewnym kiosku. W poniższej tabeli przedstawiono informacje o tym, ile osób kupiło bilety tramwajowe ulgowe oraz ile osób kupiło bilety tramwajowe normalne.

Rodzaj kupionych biletów	Liczba osób
ulgowe	76
normalne	41

Uwaga! \(27\) osób spośród ankietowanych kupiło oba rodzaje biletów.

Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że osoba losowo wybrana spośród ankietowanych nie kupiła żadnego biletu. Wynik przedstaw w formie nieskracalnego ułamka.

\(\frac{5}{23}\)

W nieskończonym ciągu arytmetycznym \((a_n)\), określonym dla \(n\ge 1\), suma jedenastu początkowych wyrazów tego ciągu jest równa \(187\). Średnia arytmetyczna pierwszego, trzeciego i dziewiątego wyrazu tego ciągu, jest równa \(12\). Wyrazy \(a_1, a_3, a_k\) ciągu \((a_n)\), w podanej kolejności, tworzą nowy ciąg - trzywyrazowy ciąg geometryczny \((b_n)\). Oblicz \(k\).

\(k=11\)