Matura 2014 luty

Cenę pralki obniżono o \( 30\% \), a po dwóch miesiącach nową cenę obniżono jeszcze o \( 20\% \). W wyniku obu obniżek cena pralki zmniejszyła się o:

Liczba \( 4\sqrt{3}-(1+2\sqrt{3})^2 \) jest równa

Wartość wyrażenia \( \vert{3-x}\vert-\vert{x+4}\vert \) dla \( x \in (3,+\infty) \) jest równa

Po uproszczeniu wyrażenia \( \frac{(a^2:a^3)^{-2}}{a^{-5}} \), gdzie \( a \ne 0 \), otrzymamy

Obwód trójkąta równobocznego o polu \( \sqrt{3} \) jest równy:

Liczba \( \left ( \log_{\sqrt{3}}3\sqrt{3} \right )^4 \) jest równa

Miejscami zerowymi funkcji \( f(x)=\frac{(x-2)(x^2-6x+9)}{x^2-9} \) są liczby:

Na trójkącie równoramiennym \( ABC \), w którym \( \vert{AC}\vert=\vert{BC}\vert \) opisano okrąg o środku \( O \). Prosta \( k \) jest styczna do tego okręgu w punkcie \( B \) i \( \vert{\sphericalangle BOC}\vert=140^\circ \). 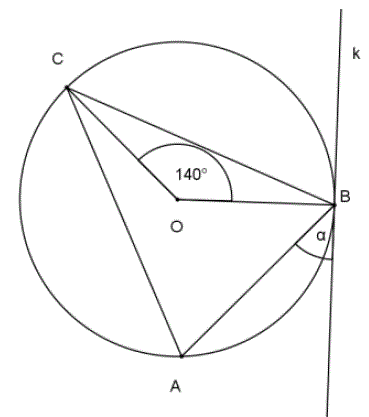Kąt \( \alpha \) ma miarę

Proste \( k \) i \( l \) są równoległe. Miara kąta \( \alpha \) wynosi:

Ciąg geometryczny \( (a_n) \) określony jest wzorem \( a_n=\frac{3^n}{4} \). Iloraz tego ciągu jest równy:

Wierzchołek paraboli, która jest wykresem funkcji \( y=x^2 -2x-3 \) leży na prostej:

Punkty \( A=(-1,2) \) i \( B=(2,6) \) są wierzchołkami kwadratu \( ABCD \). Pole tego kwadratu jest równe:

Obrazem punktu \( A=(4,-5) \) w symetrii względem osi \( Ox \) jest punkt:

W trójkącie prostokątnym najdłuższy bok ma długość \(25\), a najkrótszy \(7\). Tangens najmniejszego kąta tego trójkąta jest równy:

Miary kątów czworokąta tworzą ciąg arytmetyczny o różnicy \( 20^\circ \). Największy kąt tego czworokąta ma miarę:

\( x_1 \) jest mniejszym, zaś \( x_2 \)większym miejscem zerowym funkcji \( f(x)=2x^2+10x+12 \). Wyrażenie \( x_2-x_1 \) ma wartość:

Do wykresu funkcji \( f(x)=\frac{a}{x+1} \) określonej dla \(x\ne -1\) należy punkt \( A=(-2,3) \) dla \( a \) równego:

Wykresy funkcji liniowych \( f(x)=\frac{\sqrt{5}}{3}x+6 \) oraz \( g(x)=\frac{5}{3\sqrt{5}}x-\frac{1}{6} \) :

Środkiem okręgu o równaniu \( (x+2)^2+(y-3)^2=16 \) jest punkt:

Graniastosłup ma \( 10 \) ścian. Liczba wszystkich krawędzi tego graniastosłupa wynosi:

Liczba pierwiastków wielomianu \( W(x)=x^3-3x^2+4x-12\ \) jest równa:

Jacek rzucił pięć razy symetryczną sześcienną kostką do gry. Liczba wyrzuconych oczek wynosiła kolejno \(1, 2, 3, 4, 5\). Prawdopodobieństwo, że w szóstym rzucie wypadnie \(6\) oczek jest równe:

Jeżeli wysokość stożka zwiększymy trzykrotnie, a długość promienia zmniejszymy trzy razy, to objętość nowego stożka:

Średnia arytmetyczna wszystkich liczb pierwszych z przedziału \( \langle 1; 13 ) \) jest równa:

Przekątna ściany sześcianu ma długość \( 5\sqrt{2} \). Pole powierzchni tego sześcianu jest równe:

Rozwiąż nierówność \( (2-x)^2 \le 9 \).

Udowodnij, że reszta z dzielenia liczby \( 34429^3 \) przez \( 17 \) jest równa \( 13 \).

Oblicz długość odcinka \( x \) zaznaczonego na rysunku.

Udowodnij, że punkty \( A=(1,2), B=(-2,8)\) i \( C=(-25,54) \) są współliniowe.

Ze zbioru liczb \( {1, 2, 3, 4, 5, 6} \) losujemy dwa razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb jest liczbą podzielną przez \( 3 \).

Ciąg \( (2x – 1, y, 6x + 3)\ \) jest arytmetyczny, a ciąg \( (3, y, 27)\ \) jest geometryczny rosnący. Oblicz \(x\) i \(y\).

Drut o długości \(96\) cm wykorzystano w całości na wykonanie szkieletu ostrosłupa prawidłowego czworokątnego o wszystkich krawędziach równej długości. Zaznacz na rysunku kąt nachylenia ściany bocznej ostrosłupa do płaszczyzny podstawy i wyznacz cosinus tego kąta.

Rysunek obok przedstawia wykres funkcji kwadratowej \( f \). Zapisz wzór funkcji \( f \) w postaci ogólnej i podaj jej zbiór wartości.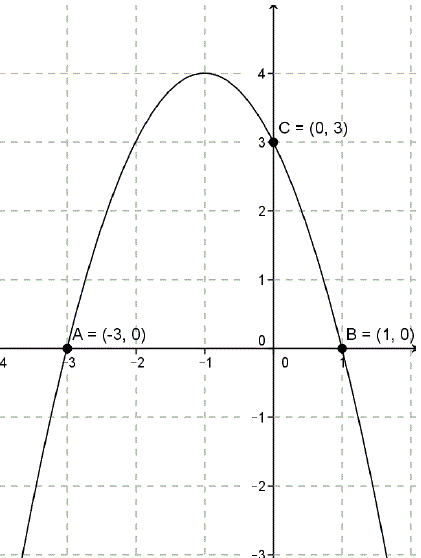

Wykwalifikowany robotnik pracując sam, wykonałby pracę w czasie krótszym o \(10\) dni od pracownika niewykwalifikowanego. Aby pracę wykonać szybciej, powierzono ją obu robotnikom, którzy pracując razem, wykonali ją w ciągu \(12\) dni. W ciągu ilu dni wykonałby pracę każdy robotnik pracując samodzielnie?