Kąt między prostymi
Twierdzenie
Jeśli proste o równaniach \(y=a_1 x+b_1\) oraz \(y=a_2 x+b_2\) przecinają się pod kątem ostrym \(\gamma \), to \[ \operatorname{tg} \gamma =\left|\frac{a_1-a_2}{1+a_1 a_2}\right| \]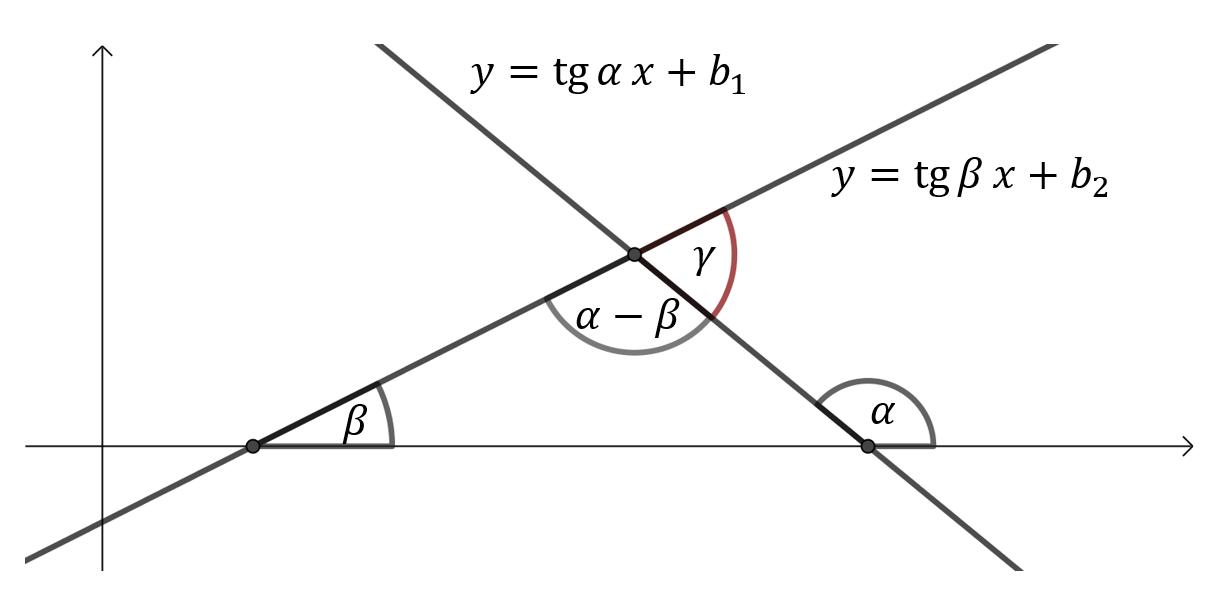
Wówczas współczynniki kierunkowe tych prostych to: \[a_1=\operatorname{tg} \alpha \quad \text{oraz}\quad a_2=\operatorname{tg} \beta \] Proste mogą przecinać się na dwa sposoby. Albo kąt ostry to \(\alpha -\beta \) i wówczas ze wzoru na tangens różnicy kątów mamy: \[\text{tg}{\left ( \alpha -\beta \right )}=\frac{\text{tg}{\alpha }-\text{tg}{\beta }}{1+\text{tg}{\alpha }\ \text{tg}{\beta }}\]
Albo kąt ostry to \(\gamma =180^\circ -(\alpha -\beta )\) i wówczas mamy: \[\operatorname{tg} \gamma = \operatorname{tg} (180^\circ -\alpha +\beta )= \operatorname{tg} (\beta-\alpha)\] Zatem: \[\operatorname{tg} \gamma =\frac{\text{tg}{\beta }-\text{tg}{\alpha }}{1+\text{tg}{\alpha }\ \text{tg}{\beta }}\]
W obu przypadkach otrzymaliśmy podobne wzory, różniące się jedynie znakiem licznika. Zatem możemy zapisać jeden wzór dla obu przypadków: \[\text{tg} \gamma=\left|\frac{\text{tg}{\alpha }-\text{tg}{\beta }}{1+\text{tg}{\alpha }\ \text{tg}{\beta }}\right|\]Moduł musi być przyłożony do całego wzoru, a nie tylko licznika, ponieważ liczymy tangens kąta ostrego, który musi być dodatni. W obu powyższych wzorach jeżeli licznik wychodzi ujemny, to i mianownik musi być ujemny, aby wynik był dodatni. Zatem nie możemy przyłożyć modułu do samego licznika.
Zatem ostatecznie mamy: \[ \operatorname{tg} \gamma =\left|\frac{a_1-a_2}{1+a_1 a_2}\right| \] co kończy dowód twierdzenia.Wyznacz kąt między prostymi o równaniach \(y=2x+1\) oraz \(y=-x+4\).
Współczynniki kierunkowe tych prostych to:
\[ a_1=2 \quad \text{oraz} \quad a_2=-1 \]Zastosujmy wzór: \[ \operatorname{tg} \gamma = \left|\frac{a_1-a_2}{1+a_1a_2}\right| \] Podstawiamy wartości: \[ \operatorname{tg} \gamma = \left|\frac{2-(-1)}{1+2\cdot(-1)}\right| = \left|\frac{3}{1-2}\right| = \left|\frac{3}{-1}\right| = 3. \]
Obliczamy miarę kąta: \[ \gamma = \arctan(3) \approx 71{,}6^\circ. \]
Zatem kąt między prostymi wynosi około \(71{,}6^\circ\).
Dla prostej \(y=2x+3\) współczynnik kierunkowy wynosi \(a_1=2\), a dla prostej \(l\) współczynnik kierunkowy wynosi \(m\). Stosujemy wzór na kąt między prostymi:
\[ \operatorname{tg} \gamma = \left|\frac{a_1-m}{1+a_1 m}\right| \]Podstawiamy \(a_1=2\) oraz \(\operatorname{tg} \gamma = \frac{1}{2}\):
\[\begin{split} \left|\frac{2-m}{1+2m}\right| &= \frac{1}{2}\\[6pt] \frac{2-m}{1+2m} = \frac{1}{2}\quad &\lor \quad \frac{2-m}{1+2m}=-\frac{1}{2}\\[6pt] \end{split} \] Rozwiążemy najpierw pierwszy przypadek: \[\begin{split} \frac{2-m}{1+2m} &= \frac{1}{2}\\[6pt] 2(2-m) &= 1+2m\\[6pt] 4-2m &= 1+2m\\[6pt] 4m &= 3\\[6pt] m &= \frac{3}{4} \end{split} \] A teraz drugi przypadek: \[\begin{split} \frac{2-m}{1+2m} &= -\frac{1}{2}\\[6pt] 2(2-m) &= -1-2m\\[6pt] 4-2m &= -1-2m\\[6pt] 4 &= -1 \end{split} \] Otrzymaliśmy sprzeczność, zatem jedyne rozwiązanie to: \[m=\frac{3}{4}\]Znajdź współczynnik kierunkowy \(a\) prostej \(l\) o równaniu \(y=ax-3\), która przecina się z prostą o równaniu \(y=5x+2\) pod kątem \(30^\circ\).
Stosujemy wzór na kąt między prostymi:
\[ \operatorname{tg} \gamma = \left|\frac{a_1-a_2}{1+a_1a_2}\right| \]Dla \(\gamma=30^\circ\) mamy \(\operatorname{tg}30^\circ=\frac{1}{\sqrt{3}}\). Stąd:
\[ \begin{split} \left|\frac{a-5}{1+5a}\right| &= \frac{1}{\sqrt{3}}\\[6pt] \frac{a-5}{1+5a} = \frac{1}{\sqrt{3}} \quad &\lor \quad \frac{a-5}{1+5a} = -\frac{1}{\sqrt{3}} \end{split} \]Przypadek 1:
\[ \begin{split} \frac{a-5}{1+5a} &= \frac{1}{\sqrt{3}}\\[6pt] \sqrt{3}(a-5) &= 1+5a\\[6pt] \sqrt{3}a - 5\sqrt{3} &= 1+5a\\[6pt] \sqrt{3}a - 5a &= 1+5\sqrt{3}\\[6pt] a(\sqrt{3}-5) &= 1+5\sqrt{3}\\[6pt] a &= \frac{1+5\sqrt{3}}{\sqrt{3}-5} \end{split} \] Usuwamy niewymierność z mianownika, mnożąc licznik i mianownik przez \(\sqrt{3}+5\): \[ \begin{split} a &= \frac{(1+5\sqrt{3})(\sqrt{3}+5)}{(\sqrt{3}-5)(\sqrt{3}+5)}\\[6pt] a &= \frac{ \sqrt{3} + 5 + 15 + 25\sqrt{3}}{3-25}\\[6pt] a &= \frac{ 20 + 26\sqrt{3}}{-22}\\[6pt] a &= -\frac{10+13\sqrt{3}}{11} \end{split} \]Przypadek 2:
\[ \begin{split} \frac{a-5}{1+5a} &= -\frac{1}{\sqrt{3}}\\[6pt] \sqrt{3}(a-5) &= -1-5a\\[6pt] \sqrt{3}a - 5\sqrt{3} &= -1-5a\\[6pt] \sqrt{3}a +5a &= 5\sqrt{3}-1\\[6pt] a(\sqrt{3}+5) &= 5\sqrt{3}-1\\[6pt] a &= \frac{5\sqrt{3}-1}{\sqrt{3}+5} \end{split} \] Usuwamy niewymierność z mianownika mnożąc licznik i mianownik przez \(\sqrt{3}-5\): \[ \begin{split} a &= \frac{(5\sqrt{3}-1)(\sqrt{3}-5)}{(\sqrt{3}+5)(\sqrt{3}-5)}\\[6pt] a &= \frac{ 5\sqrt{3}\cdot\sqrt{3} - 5\sqrt{3}\cdot5 - 1\cdot\sqrt{3} + 1\cdot5}{3-25}\\[6pt] a &= \frac{20 - 26\sqrt{3}}{-22}\\[6pt] a &= \frac{13\sqrt{3}-10}{11} \end{split} \] Ostatecznie otrzymujemy dwa rozwiązania: \[ a = -\frac{10+13\sqrt{3}}{11} \quad \text{lub} \quad a = \frac{13\sqrt{3}-10}{11} \]