Funkcja wykładnicza i jej własności
Poziom podstawowy
Definicja
Funkcję postaci \(f(x)=a^x\), gdzie \(a \gt 0\) i \(a\ne 1\), określoną dla \(x\in \mathbb{R} \), nazywamy funkcją wykładniczą. Nazwa funkcji wykładniczej pochodzi od tego, że argument \(x\) znajduje się w wykładniku.
Wykres funkcji \(f(x) = a^x\) zawsze przecina oś \(y\)-ów w punkcie \((0,1)\).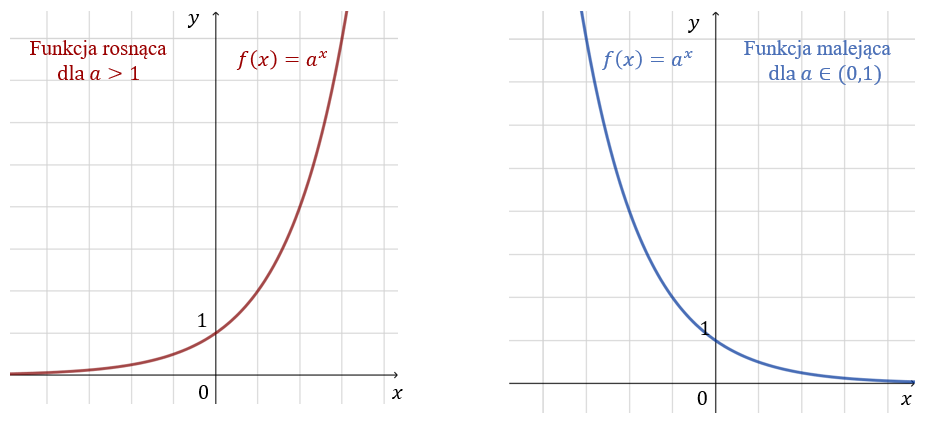 
Wykres funkcji \(f(x) = 2^x\) szkicujemy obliczając wartości funkcji w tabelce:
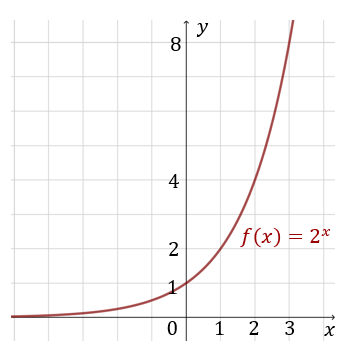Jest to funkcja rosnąca, a jej zbiorem wartości jest przedział \((0, +\infty )\).
| \(x\) | \(-3\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) |
| \(f(x)=2^x\) | \(\frac{1}{8}\) | \(\frac{1}{4}\) | \(\frac{1}{2}\) | \(1\) | \(2\) | \(4\) | \(8\) |
Jest to funkcja rosnąca, a jej zbiorem wartości jest przedział \((0, +\infty )\). Przykłady kilku różnych funkcji wykładniczych o podstawie \(a\gt 1\):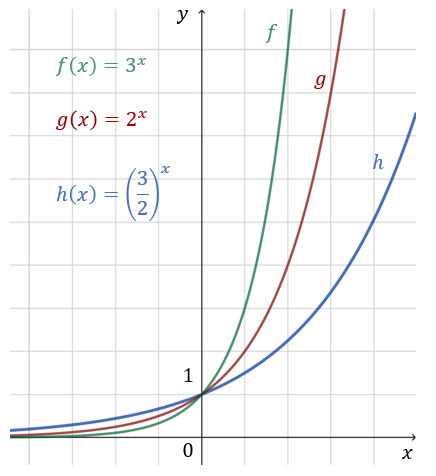 
Narysujemy wykres funkcji \(y=\left(\frac{1}{2}\right)^x\).
Na początek obliczmy wartości tej funkcji dla kilku przykładowych argumentów \(x\). Sporządźmy zatem odpowiednią tabelkę:
i rysujemy wykres: 
Jest to funkcja malejąca, a jej zbiorem wartości jest przedział \((0, +\infty )\).
Na początek obliczmy wartości tej funkcji dla kilku przykładowych argumentów \(x\). Sporządźmy zatem odpowiednią tabelkę:
| \(x\) | \(-3\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) |
| \(y=\left(\frac{1}{2}\right)^x\) | \(8\) | \(4\) | \(2\) | \(1\) | \(\frac{1}{2}\) | \(\frac{1}{4}\) | \(\frac{1}{8}\) |
Jest to funkcja malejąca, a jej zbiorem wartości jest przedział \((0, +\infty )\). Przykłady kilku różnych funkcji wykładniczych o podstawie \(a \lt 1\):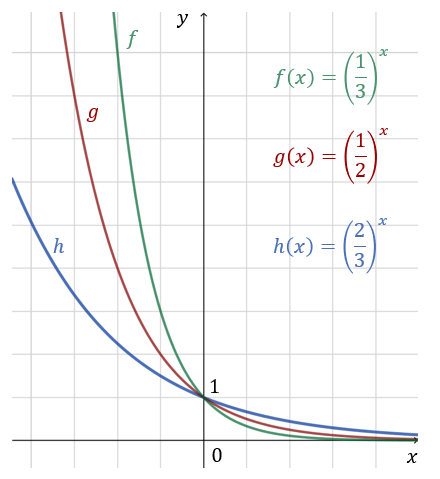 
Własności funkcji wykładniczej \(f(x)=a^x\)
- Dziedzina: \(\mathbb{R} \).
- Zbiór wartości: \((0, +\infty )\).
- Dla \(a\gt 1\) funkcja jest rosnąca, a dla \(a\in (0,1)\) malejąca.
- Funkcja jest różnowartościowa.
- Funkcja przyjmuje tylko wartości dodatnie: \(f(x)\gt 0,\ \text{dla}\ x\in \mathbb{R} \)
- Funkcja nie ma miejsc zerowych.
- Funkcja nie jest parzysta i nie jest nieparzysta.
Oblicz wartości funkcji \(f\) dla \(x \in\left\{3, -2, \frac{1}{2}, -\frac{1}{2} \right\}\).
\(f(x)=3^x\)
\(f(x)=\left(\frac{1}{9}\right)^x\)
\(f(x)=4^x\)
\(f(x)=\left(\frac{1}{2}\right)^x\)
Punkt \(P=(2,25)\) należy do wykresu funkcji wykładniczej \(f(x)=a^x\). Czy punkt \(B\) też należy do wykresu funkcji \(f\)?
\(B=\left(\frac{1}{2}, \sqrt{5}\right)\)
\(B=(3,100)\)
\(B=\left(-3,\frac{1}{125}\right)\)
\(B=\left(-\frac{1}{5},1\right)\)
Do wykresu funkcji wykładniczej \(f(x)=a^x\) należy punkt \(P\). Określ monotoniczność tej funkcji.
\(P=(-3,8)\)
\(P=\left(\frac{1}{2}, 10\right)\)
\(P=\left(1, \sqrt{7}-\sqrt{3}\right)\)
\(P=\left(-2, 3-\sqrt{3}\right)\)
Wyznacz trzy punkty o współrzędnych wymiernych należące do wykresu funkcji wykładniczej \(f\). Naszkicuj wykres funkcji \(f\).
\(f(x)=(\sqrt{5})^x\)
\(f(x)=\left(\frac{\sqrt{3}}{7}\right)^x\)
\(f(x)=(\sqrt[3]{2})^x\)
Podaj zbiór rozwiązań nierówności, korzystając z odpowiednich wykresów
\(2^x\gt 3^x\)
\(2^x \leqslant 3^x\)
\(\left(\frac{1}{2}\right)^x \leqslant\left(\frac{1}{3}\right)^x\)
\(\left(\frac{1}{3}\right)^x\gt 2^x\)
Zapisz liczby \(x, y, z\) w kolejności od najmniejszej do największej:
\(x=5^\sqrt{5}\), \(\ y=5^{2{,}2}\), \(\ z=5^{\pi}\)
\(x=(0{,}9)^{1{,}4}\), \(\ y=(0{,}9)^{0{,}9}\), \(\ z=\left((0{,}9)^{0{,}9}\right)^{1{,}5}\)
\(x=(\sqrt{2}-1)^{\pi}\), \(\ y=\frac{1}{\left(\sqrt{2}+1\right)^3}\), \(\ z=\left(\frac{2-\sqrt{2}}{\sqrt{2}}\right)^{\sqrt{2}}\)
Funkcja \(f\) jest określona wzorem \(f(x) =\left(\frac{1}{2}\right)^x\) dla wszystkich liczb rzeczywistych \(x\). Funkcja \(f\) dla argumentu \(x =-3\) przyjmuje wartość
A.\( \frac{1}{6} \)
B.\( \frac{1}{8} \)
C.\( 6 \)
D.\( 8 \)
Na rysunku przedstawiono fragment wykresu funkcji wykładniczej \(f\) określonej wzorem \(f(x)=a^x\). Punkt \(A=(1,2)\) należy do wykresu funkcji. 
Podstawa \(a\) potęgi jest równa
Podstawa \(a\) potęgi jest równa A.\( -\frac{1}{2} \)
B.\( \frac{1}{2} \)
C.\( -2 \)
D.\( 2 \)
Do wykresu funkcji \(f\) określonej dla każdej liczby rzeczywistej \(x\) wzorem \(f(x)=3^x-2\) należy punkt o współrzędnych
A.\( (-1,-5) \)
B.\( (0,-2) \)
C.\( (0,-1) \)
D.\( (2,4) \)
Do wykresu funkcji wykładniczej \(f(x)=\left(\frac{1}{4}\right)^x\) należy punkt
A.\( A=\left(-\frac{1}{2},-2\right) \)
B.\( A=\left(-\frac{1}{2},2\right) \)
C.\( A=\left(2,\frac{1}{2}\right) \)
D.\( A=\left(2,-\frac{1}{2}\right) \)
Funkcja wykładnicza określona wzorem \(f(x)=3^x\) przyjmuje wartość \(6\) dla argumentu
A.\( x=2 \)
B.\( x=\log_{3}2 \)
C.\( x=\log_{3}6 \)
D.\( x=\log_{6}3 \)
Do wykresu funkcji, określonej dla wszystkich liczb rzeczywistych wzorem \( y=-2^{x-2} \), należy punkt
A.\(A=(1,-2) \)
B.\(B=(2,-1) \)
C.\(C=(1,\frac{1}{2}) \)
D.\(D=(4,4) \)
Tematy nadrzędne i sąsiednie