Czworościan foremny

Drukuj

Poziom podstawowy

Czworościan foremny - to taki ostrosłup, który ma w podstawie oraz ścianach bocznych trójkąty równoboczne.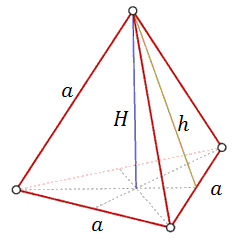

Wzór na pole powierzchni czworościanu foremnego: \[P_c=a^2\sqrt{3}\] Wzór na objętość czworościanu foremnego: \[V=\frac{a^3\sqrt{2}}{12}\] Wzór na wysokość czworościanu foremnego: \[H=\frac{a\sqrt{6}}{3}\] Wzór na wysokość ściany bocznej czworościanu foremnego: \[h=\frac{a\sqrt{3}}{2}\]

Każda krawędź ostrosłupa prawidłowego trójkątnego ma długość \(9\) (ostrosłup taki jest nazywany czworościanem foremnym). Wysokość tego ostrosłupa jest równa

A.\( 3\sqrt{6} \)

B.\( 3\sqrt{3} \)

C.\( 2\sqrt{6} \)

D.\( 3\sqrt{2} \)

Poziom rozszerzony

W czworościanie, którego wszystkie krawędzie maja taką samą długość \(6\), umieszczono kulę tak, że ma ona dokładnie jeden punkt wspólny z każdą ścianą czworościanu. Płaszczyzna \(\pi\), równoległa do podstawy tego czworościanu, dzieli go na dwie bryły: ostrosłup o objętości równej \(\frac{8}{27}\) objętości dzielonego czworościanu i ostrosłup ścięty. Oblicz odległość środka \(S\) kuli od płaszczyzny \(\pi\), tj. długość najkrótszego spośród odcinków \(SP\), gdzie \(P\) jest punktem płaszczyzny \(\pi\).