Czworokąt

Drukuj

Poziom podstawowy

Narysujmy dowolny czworokąt i wprowadźmy na nim następujące oznaczenia: 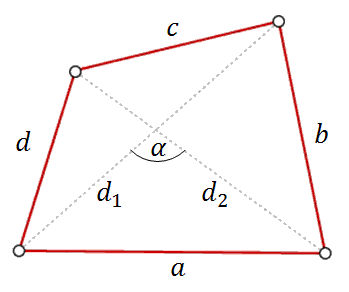rysunek czworokąta z oznaczeniami

Wzór na obwód i pole: \[Ob = a+b+c+d\\[6pt] P=\frac{1}{2}d_1\cdot d_2\cdot \sin \alpha \] gdzie:

\(a\), \(b\), \(c\), \(d\) - to boki czworokąta,
\(d_1\), \(d_2\) - to przekątne czworokąta,
\(\alpha \) - to kąt między przekątnymi czworokąta.

Obwód czworokąta wypukłego \(ABCD\) jest równy \(50\) cm. Obwód trójkąta \(ABD\) jest równy \(46\) cm, a obwód trójkąta \(BCD\) jest równy \(36\) cm. Oblicz długość przekątnej \(BD\).

\(|BD|=16\)

Dany jest czworokąt \(ABCD\), w którym \(AB \parallel CD\). Na boku \(BC\) wybrano taki punkt \(E\), że \(|EC|=|CD|\) i \(|EB|=|BA|\). Wykaż, że kąt \(AED\) jest prosty.