Asymptoty wykresu funkcji

Drukuj

Poziom studiów

Asymptota – to prosta, do której dąży wykres funkcji w nieskończoności lub w otoczeniu punktu, który nie należy do dziedziny funkcji.
Wyróżniamy trzy rodzaje asymptot:

pionowa,
pozioma,
ukośna.

Asymptoty nie są częścią wykresu funkcji, tylko stanowią linie pomocnicze przy jego szkicowaniu.

Oto przykład wykresu funkcji z asymptotami pionową oraz poziomą: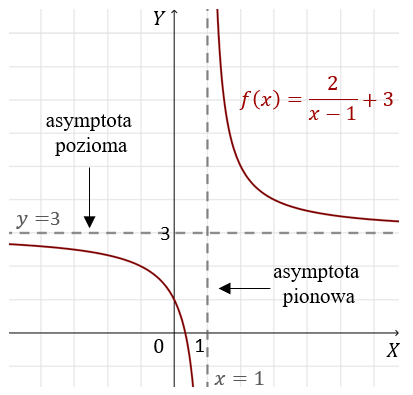

A to przykład z asymptotą ukośną:

Asymptota pozioma

Niech funkcja \(f\) będzie określona w nieskończonościach.
Prostą \(y=b\) nazywamy:

asymptotą poziomą w plus nieskończoności, jeżeli: \[\lim _{x \to +\infty} f(x)=b\]
asymptotą poziomą w minus nieskończoności, jeżeli: \[\lim _{x \to -\infty} f(x)=b\]

Jeśli asymptota pozioma w plus i minus nieskończoności ma to samo równanie, to nazywamy ją asymptotą poziomą obustronną.

Asymptota pionowa

Niech funkcja \(f\) będzie określona w otoczeniu argumentu \(x_0\).
Prostą \(x=x_0\) nazywamy:

asymptotą pionową prawostronną, jeżeli: \[\lim_{x \rightarrow x_0^{+}} f(x)= \pm \infty\]
asymptotą pionową lewostronną, jeżeli: \[\lim_{x \rightarrow x_0^{-}} f(x)= \pm \infty\]

Jeżeli w punkcie \(x_0\) funkcja ma asymptotę pionową prawostronną i lewostronną, to nazywamy ją asymptotą pionową obustronną

Wyznacz asymptoty poziome i pionowe funkcji \(f(x)=\frac{1}{x-2}\).

Dziedzina funkcji \(f(x)\) to: \(x\in \mathbb{R} \backslash \{2\}\).
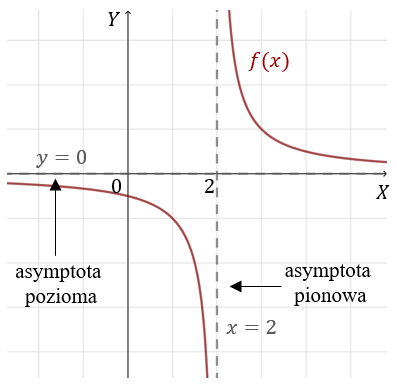
Sprawdzamy czy istnieje asymptota pionowa w punkcie \(x_0=2\). Liczymy granice jednostronne: \[\lim _{x \rightarrow 2^{+}} \frac{1}{x-2}=\left[\frac{1}{0^+ }\right]+\infty\] oraz \[\lim _{x \rightarrow 2^{-}} \frac{1}{x-2}=\left[\frac{1}{0^-}\right]=-\infty\] Zatem prosta \(x=2\) jest asymptotą pionową (obustronną).

Teraz wyznaczymy asymptoty poziome. Liczymy granice funkcji w nieskończonościach: \[\lim _{x \to +\infty} \frac{1}{x-2}=\left[\frac{1}{\infty }\right]=0\] \[\lim _{x \to -\infty} \frac{1}{x-2}=\left[\frac{1}{-\infty }\right]=0\] Zatem prosta \(y=0\) jest asymptotą poziomą (obustronną).

Teraz możemy naszkicować wykres:

Wyznacz asymptoty poziome i pionowe funkcji \(f(x)=\frac{2}{3x-1} + 5\).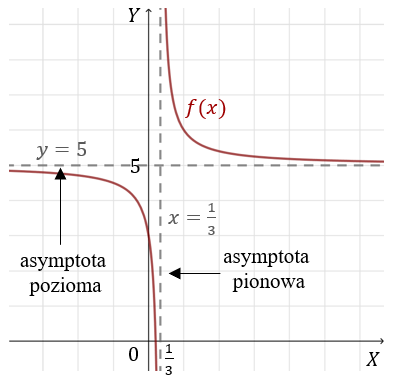

Dziedzina funkcji \(f(x)\) to: \(x\in \mathbb{R} \backslash \left\{\frac{1}{3}\right\}\).
Sprawdzamy, czy istnieje asymptota pionowa w punkcie \(x_0=\frac{1}{3}\). Liczymy granice jednostronne: \[ \lim _{x \to \frac{1}{3}^{+}} \left( \frac{2}{3x-1} + 5 \right) = \frac{2}{0^+} + 5 = +\infty, \] oraz \[ \lim _{x \to \frac{1}{3}^{-}} \left( \frac{2}{3x-1} + 5 \right) = \frac{2}{0^-} + 5 = -\infty. \] Zatem prosta \(x=\frac{1}{3}\) jest asymptotą pionową (obustronną).

Teraz wyznaczymy asymptoty poziome. Liczymy granice funkcji w nieskończonościach: \[ \lim _{x \to +\infty} \left( \frac{2}{3x-1} + 5 \right) = \frac{2}{\infty} + 5 = 5, \] \[ \lim _{x \to -\infty} \left( \frac{2}{3x-1} + 5 \right) = \frac{2}{-\infty} + 5 = 5. \] Zatem prosta \(y=5\) jest asymptotą poziomą (obustronną).

Teraz możemy naszkicować wykres:

Wyznacz asymptoty poziome i pionowe funkcji \(f(x)=\frac{1}{x^2 - 9} - 2\).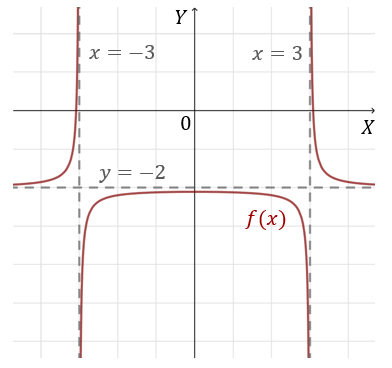

Dziedzina funkcji \(f(x)\) to: \(x\in \mathbb{R} \backslash \{-3, 3\}\), ponieważ \(x^2 - 9 = 0\) dla \(x = \pm 3\).
Sprawdzamy, czy istnieją asymptoty pionowe w punktach \(x_1 = 3\) i \(x_2 = -3\). Liczymy granice jednostronne: \[ \lim _{x \to 3^{+}} \left( \frac{1}{x^2 - 9} - 2 \right) = \frac{1}{0^+} - 2 = +\infty, \] \[ \lim _{x \to 3^{-}} \left( \frac{1}{x^2 - 9} - 2 \right) = \frac{1}{0^-} - 2 = -\infty. \] Zatem prosta \(x=3\) jest asymptotą pionową (obustronną).
Liczymy podobnie dla \(x_2 = -3\): \[ \lim _{x \to -3^{+}} \left( \frac{1}{x^2 - 9} - 2 \right) = \frac{1}{0^+} - 2 = +\infty, \] \[ \lim _{x \to -3^{-}} \left( \frac{1}{x^2 - 9} - 2 \right) = \frac{1}{0^-} - 2 = -\infty. \] Zatem prosta \(x=-3\) również jest asymptotą pionową (obustronną).

Teraz wyznaczymy asymptoty poziome. Liczymy granice funkcji w nieskończonościach: \[ \lim _{x \to +\infty} \left( \frac{1}{x^2 - 9} - 2 \right) = \frac{1}{\infty} - 2 = -2, \] \[ \lim _{x \to -\infty} \left( \frac{1}{x^2 - 9} - 2 \right) = \frac{1}{\infty} - 2 = -2. \] Zatem prosta \(y=-2\) jest asymptotą poziomą (obustronną).

Oto wykres tej funkcji z zaznaczonymi asymptotami:

Asymptota ukośna

Niech funkcja \(f\) będzie określona w przedziale \((-\infty, c)\), gdzie \(c \in \mathbb{R}\).
Prosta \(y=ax+b\) jest:

asymptotą ukośną lewostronną, jeżeli: \[\lim _{x \rightarrow-\infty}[f(x)-(ax+b)]=0\]
asymptotą ukośną prawostronną, jeżeli: \[\lim _{x \rightarrow+\infty}[f(x)-(ax+b)]=0\]

Przy wyznaczaniu asymptot ukośnych można korzystać bezpośrednio z powyższej definicji, ale często wygodniejszym rozwiązaniem jest skorzystanie z poniższego twierdzenia.

Twierdzenie

Prosta \(y=ax+b\) jest:

asymptotą ukośną lewostronną wtedy i tylko wtedy, gdy \[ a=\lim _{x \rightarrow -\infty} \frac{f(x)}{x} \] oraz \[b=\lim _{x \rightarrow -\infty}[f(x)-ax]\]
asymptotą ukośną prawostronną wtedy i tylko wtedy, gdy \[ a=\lim _{x \rightarrow +\infty} \frac{f(x)}{x} \] oraz \[b=\lim _{x \rightarrow +\infty}[f(x)-ax]\]

i granice te są skończone.

Wyznacz asymptoty pionowe, poziome i ukośne funkcji \(f(x)=\frac{1 - x^2}{2x - 4} - 3\).

Dziedzina funkcji \(f(x)\) to: \(x \in \mathbb{R} \backslash \{2\}\), ponieważ mianownik \(2x - 4 = 0\) dla \(x = 2\).
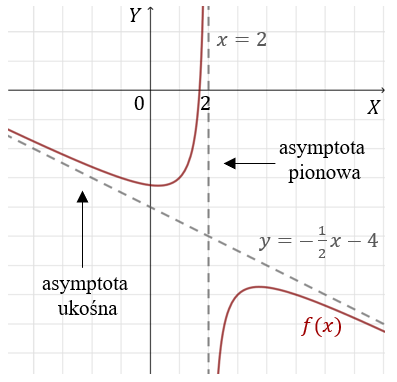
Sprawdzamy, czy istnieje asymptota pionowa w punkcie \(x_0=2\). Liczymy granice jednostronne: \[ \lim _{x \to 2^{+}} \left( \frac{1 - x^2}{2x - 4} - 3 \right) = \frac{-3}{0^+} - 3 = -\infty, \] \[ \lim _{x \to 2^{-}} \left( \frac{1 - x^2}{2x - 4} - 3 \right) = \frac{-3}{0^-} - 3 = +\infty. \] Zatem prosta \(x=2\) jest asymptotą pionową (obustronną).

Teraz wyznaczymy asymptoty poziome. Liczymy granice funkcji w nieskończonościach:

\[\lim _{x \to +\infty} \left( \frac{1 - x^2}{2x - 4} - 3 \right) = \lim _{x \to +\infty} \left( \frac{\frac{1}{x}-x}{2-\frac{4}{x}} \right) - 3 = -\infty\] \[\lim _{x \to -\infty} \left( \frac{1 - x^2}{2x - 4} - 3 \right) = \lim _{x \to -\infty} \left( \frac{\frac{1}{x}-x}{2-\frac{4}{x}} \right) - 3 = +\infty\]

Funkcja nie ma asymptot poziomych, ponieważ granice dążą do \( \pm\infty \).

Sprawdzamy, czy funkcja posiada asymptotę ukośną lewostronną \(y=ax+b\).
W tym celu liczymy granicę:

\[\lim _{x \rightarrow -\infty} \frac{f(x)}{x}= \lim _{x \rightarrow -\infty} \frac{1 - x^2}{2x^2 - 4x}-\frac{3}{x} = -\frac{1}{2} -0-=-\frac{1}{2}\]

\[\begin{split} \lim _{x \rightarrow -\infty} \frac{f(x)}{x}&= \lim _{x \rightarrow -\infty} \frac{1 - x^2}{2x^2 - 4x}-\frac{3}{x}=\\[6pt] &= -\frac{1}{2} -0=-\frac{1}{2} \end{split}\]

Otrzymaliśmy granicę skończoną, zatem współczynnik kierunkowy szukanej prostej to \(a=-\frac{1}{2}\).
Teraz szukamy współczynnika \(b\) licząc granicę:

\[\begin{split} \lim _{x \rightarrow -\infty}(f(x)-ax) &= \lim _{x \rightarrow -\infty} \frac{1 - x^2}{2x - 4} - 3 - \left(-\frac{1}{2}\right)x = \lim _{x \rightarrow -\infty} \frac{1 - x^2}{2x - 4}+\frac{x(x-2)}{2x-4}-3=\\[6pt] &= \lim _{x \rightarrow -\infty} \frac{1 - x^2+x^2-2x}{2x - 4}-3 = \lim _{x \rightarrow -\infty} \frac{-2x+1}{2x - 4}-3 = \frac{-2}{2}-3 = -4 \end{split}\]

\[\begin{split} &\lim _{x \rightarrow -\infty}(f(x)-ax)=\\[6pt] &= \lim _{x \rightarrow -\infty} \frac{1 - x^2}{2x - 4} - 3 - \left(-\frac{1}{2}\right)x =\\[6pt] &= \lim _{x \rightarrow -\infty} \frac{1 - x^2}{2x - 4}+\frac{x(x-2)}{2x-4}-3=\\[6pt] &= \lim _{x \rightarrow -\infty} \frac{1 - x^2+x^2-2x}{2x - 4}-3=\\[6pt] &= \lim _{x \rightarrow -\infty} \frac{-2x+1}{2x - 4} -3= \frac{-2}{2} -3 = -4 \end{split}\]

Otrzymaliśmy granicę skończoną, zatem \(b=-4\). Więc asymptotą ukośną lewostronną jest prosta: \[y = -\frac{x}{2} - 4\] Teraz tak samo sprawdzamy, czy funkcja posiada asymptotę ukośną prawostronną \(y=ax+b\).
W tym celu liczymy granice (korzystając przy tym z wcześniejszych rachunków): \[\lim _{x \rightarrow +\infty} \frac{f(x)}{x}=\lim _{x \rightarrow +\infty} \frac{1 - x^2}{2x^2 - 4x}-\frac{3}{x}=-\frac{1}{2}\] oraz: \[\lim _{x \rightarrow +\infty}(f(x)-ax) = \lim _{x \rightarrow +\infty}\frac{-2x+1}{2x - 4}-3=-4 \] Zatem \(b=-4\).
Czyli funkcja posiada asymptotę ukośną prawostronną taką samą jak lewostronną: \[y = -\frac{x}{2} - 4\]

Oto wykres:

W filmie pokazuję co to są asymptoty funkcji oraz jak je wyznaczać.

Czas nagrania: 34 min.

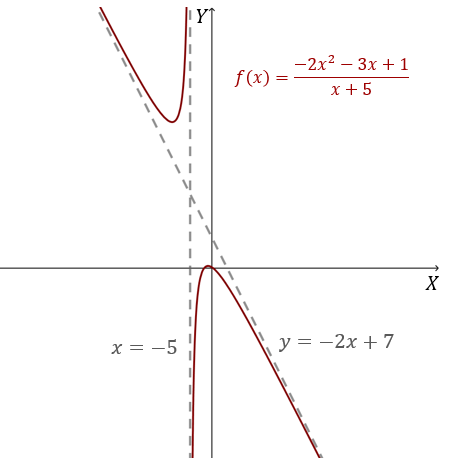
Wyznacz asymptoty pionowe, poziome i ukośne funkcji \(f(x) = \frac{-2x^2 - 3x + 1}{x + 5}\).

Dziedzina funkcji, to: \( x \in \mathbb{R} \backslash \{-5\}\).
Sprawdzamy, czy istnieje asymptota pionowa w punkcie \(x_0 = -5\). Liczymy granice jednostronne:

\[ \lim _{x \to -5^{+}} \frac{-2x^2 - 3x + 1}{x + 5} = \frac{-50 + 15 + 1}{0^+} = \frac{-34}{0^+} = -\infty, \]

\[ \begin{split} &\lim _{x \to -5^{+}} \frac{-2x^2 - 3x + 1}{x + 5} = \frac{-50 + 15 + 1}{0^+} = \\[6pt] &=\frac{-34}{0^+} = -\infty, \end{split} \]

oraz: \[ \lim _{x \to -5^{-}} \frac{-2x^2 - 3x + 1}{x + 5} = \frac{-34}{0^-} = +\infty \] Zatem prosta \(x = -5\) jest asymptotą pionową (obustronną).

Sprawdzamy czy istnieje asymptota pozioma. Liczymy granice funkcji w nieskończonościach:

\[ \lim _{x \to +\infty} \frac{-2x^2 - 3x + 1}{x + 5} = \lim _{x \to +\infty} \frac{-2x - 3 + \frac{1}{x}}{1 + \frac{5}{x}} = -\infty \]

\[\begin{split} &\lim _{x \to +\infty} \frac{-2x^2 - 3x + 1}{x + 5} = \\[6pt] &=\lim _{x \to +\infty} \frac{-2x - 3 + \frac{1}{x}}{1 + \frac{5}{x}} = -\infty \end{split} \]

Analogicznie: \[ \lim _{x \to -\infty} \frac{-2x^2 - 3x + 1}{x + 5} = +\infty \] Funkcja nie posiada asymptot poziomych, ponieważ granice w \( \pm \infty \) dążą do nieskończoności.

Funkcja może mieć asymptotę ukośną \(y = ax + b\), ponieważ w liczniku mamy wyrażenie stopnia o \(1\) większego niż w mianowniku.
Liczymy współczynniki \(a\) i \(b\): \[ \lim_{x \to \pm\infty} \frac{f(x)}{x} = \lim_{x \to \pm\infty} \frac{-2x^2 - 3x + 1}{x(x + 5)} = -2. \] Zatem \(a = -2\).
Teraz obliczamy współczynnik \(b\):

\[\begin{split} &\lim_{x \to \pm\infty} \left(f(x) - ax\right) = \lim_{x \to \pm\infty} \left(\frac{-2x^2 - 3x + 1}{x + 5} - (-2x)\right) =\\[6pt] &=\lim_{x \to \pm\infty} \left(\frac{-2x^2 - 3x + 1 + 2x(x + 5)}{x + 5}\right) = \lim_{x \to \pm\infty} \left(\frac{1+7x}{x + 5}\right) = 7. \end{split}\]

\[\begin{split} &\lim_{x \to \pm\infty} \left(f(x) - ax\right) =\\[6pt] &=\lim_{x \to \pm\infty} \left(\frac{-2x^2 - 3x + 1}{x + 5} - (-2x)\right) =\\[6pt] &=\lim_{x \to \pm\infty} \left(\frac{-2x^2 - 3x + 1 + 2x(x + 5)}{x + 5}\right) =\\[6pt] &=\lim_{x \to \pm\infty} \left(\frac{1+7x}{x + 5}\right) = 7. \end{split}\]

Zatem \(b=7\).
Zatem asymptotą ukośną jest: \[ y = -2x+7. \] Oto wykres: