Poziom rozszerzony
Rozwiązania zadań tutaj:
Rozwiązania i zasady oceniania CKE.
Dane są liczby \(a = \log_23\) oraz \(b = \log_37\).
Wyraź \(\log_449\) za pomocą liczb \(a\) oraz \(b\).
Zapisz obliczenia.
\(\log_449=a\cdot b\)
Przekształcamy \(\log _4 49\), stosując wzór na logarytm potęgi oraz wzór na zamianę podstawy logarytmu, i otrzymujemy \[\begin{align} \log _4 49=2 \cdot \log _4 7=2 \cdot \frac{\log _3 7}{\log _3 4}=2 \cdot \frac{\log _3 7}{\frac{\log _2 4}{\log _2 3}}=2 \cdot \log _3 7 \cdot \frac{\log _2 3}{\log _2 4}=2 \cdot \log _3 7 \cdot \frac{\log _2 3}{2} \end{align}\] Zatem \[ \log _4 49=2 \cdot b \cdot \frac{a}{2}=a \cdot b \] Odp. \(\log _4 49=a \cdot b\)
Funkcja \(f\) jest określona wzorem \(f(x)=\frac{x^2+3}{x-1}\) dla każdej liczby rzeczywistej \(x \ne 1\).
Wyznacz równanie stycznej do wykresu tej funkcji w punkcie \(P=(-3,-3)\).
Zapisz obliczenia.
\(y=\frac{3}{4}x-\frac{3}{4}\)
Wyznaczamy pochodną funkcji \(f\) : \[ f^{\prime}(x)=\frac{2 x \cdot(x-1)-\left(x^2+3\right) \cdot 1}{(x-1)^2}=\frac{x^2-2 x-3}{(x-1)^2} \] dla każdego \(x \in \mathbb{R} \backslash\{1\}\). Obliczamy współczynnik kierunkowy szukanej stycznej: \[ f^{\prime}(-3)=\frac{(-3)^2-2 \cdot(-3)-3}{(-3-1)^2}=\frac{9+6-3}{16}=\frac{3}{4} \] Zatem równanie stycznej do wykresu funkcji \(f\) w punkcie \(P=(-3,-3)\) ma postać: \[ y=\frac{3}{4} x+b \] Obliczamy współczynnik \(b\).
Punkt \(P\) leży na prostej stycznej, więc: \[-3=\frac{3}{4} \cdot(-3)+b\] Stąd:\[b=-\frac{3}{4}\] Zatem równanie stycznej do wykresu funkcji \(f\) w punkcie \(P=(-3,-3)\) ma postać: \[y=\frac{3}{4} x-\frac{3}{4}\]
Dany jest nieskończony ciąg geometryczny \((a_n)\), określony dla każdej liczby naturalnej \(n \ge 1\). Suma trzech początkowych wyrazów ciągu \((a_n)\) jest równa \(7\), a suma \(S\) wszystkich wyrazów tego ciągu jest równa \(8\).
Wyznacz wszystkie wartości \(n\), dla których spełniona jest nierówność \[\left|\frac{S-S_n}{S_n}\lt0{,}001\right|\] gdzie \(S_n\) oznacza sumę \(n\) początkowych wyrazów ciągu \((a_n)\).
Zapisz obliczenia.
\(n\gt9\)
Suma wszystkich wyrazów ciągu \(\left(a_n\right)\) istnieje i jest różna od zera, zatem \(a_1 \neq 0\) i iloraz \(q\) tego ciągu spełnia warunek \(|q|<1\).
Korzystamy ze wzorów na sumę \(n\) początkowych wyrazów ciągu geometrycznego oraz na sumę wszystkich wyrazów ciągu geometrycznego i obliczamy iloraz \(q\) ciągu \(\left(a_n\right)\) : \[ \begin{gathered} a_1+a_2+a_3=a_1 \cdot \frac{1-q^3}{1-q}=\frac{a_1}{1-q} \cdot\left(1-q^3\right)=S \cdot\left(1-q^3\right) \\ 7=8\left(1-q^3\right) \\ q=\frac{1}{2} \end{gathered} \] Zatem \[S=a_1 \cdot \frac{1}{1-\frac{1}{2}}=2 a_1\] i \[S_n=a_1 \cdot \frac{1-\left(\frac{1}{2}\right)^n}{1-\frac{1}{2}}=2 a_1 \cdot\left[1-\left(\frac{1}{2}\right)^n\right]\] Stąd, wobec \(a_1 \neq 0\), otrzymujemy \[\frac{S-S_n}{S_n}=\frac{2 a_1-2 a_1 \cdot\left[1-\left(\frac{1}{2}\right)^n\right]}{2 a_1 \cdot\left[1-\left(\frac{1}{2}\right)^n\right]}=\frac{2 a_1 \cdot\left(\frac{1}{2}\right)^n}{2 a_1 \cdot\left[1-\left(\frac{1}{2}\right)^n\right]}=\frac{\left(\frac{1}{2}\right)^n}{1-\left(\frac{1}{2}\right)^n}\] Rozwiązujemy nierówność \(\left|\frac{S-S_n}{S_n}\right|<0,001\) w zbiorze liczb całkowitych dodatnich: \[ \begin{gathered} \left|\frac{S-S_n}{S_n}\right|<0,001 \\ \left|\frac{\left(\frac{1}{2}\right)^n}{1-\left(\frac{1}{2}\right)^n}\right|<0,001 \end{gathered} \] Ponieważ \(q=\frac{1}{2} \in(0,1)\), więc \(1-\left(\frac{1}{2}\right)^n>0\).
Zatem nierówność \(\left|\frac{\left(\frac{1}{2}\right)^n}{1-\left(\frac{1}{2}\right)^n}\right|<0,001\) możemy przeksztakcić do postaci \[\frac{\left(\frac{1}{2}\right)^n}{1-\left(\frac{1}{2}\right)^n}<0,001\] Stąd otrzymujemy dalej: \[ \begin{gathered} \left(\frac{1}{2}\right)^n<0,001\left[1-\left(\frac{1}{2}\right)^n\right] / \cdot 2^n \\ 1<0,001\left(2^n-1\right) \\ 2^n>1001 \end{gathered} \] Ponieważ \(2^9=512\) i \(2^{10}=1024\), więc \(n>9\).
Rozwiązaniem nierówności \(\left|\frac{S-S_n}{S_n}\right|<0,001\) w zbiorze liczb całkowitych dodatnich są wszystkie liczby naturalne większe od 9 .
Dane jest równanie \((x - 6) ⋅ \bigl[(m - 2)x^2 - 4(m + 3)x + m + 1\bigl] = 0\) z niewiadomą \(x\) i parametrem \(m\in \mathbb{R}\).
Wyznacz wszystkie wartości parametru \(m\), dla których to równanie ma trzy różne rozwiązania rzeczywiste tego samego znaku.
Zapisz obliczenia.
\(m\in \left(-\infty ,-\frac{19}{3}\right)\cup (2, 11)\cup (11, +\infty )\)
Rozwiązanie CKE:
Zauważmy, że jednym z rozwiązań równania \[ (1)\qquad (x-6) \cdot\left[(m-2) x^2-4(m+3) x+m+1\right]=0 \] jest liczba 6. Zatem równanie (1) ma trzy różne rozwiązania rzeczywiste tego samego znaku wtedy i tylko wtedy, gdy równanie \[ (2)\qquad (m-2) x^2-4(m+3) x+m+1=0 \] ma dokładnie dwa różne rozwiązania dodatnie \(x_1, x_2\) takie, że \(x_1 \neq 6\) i \(x_2 \neq 6\). Dla \(m=2\) równanie (2) przyjmuje postać \(-20 x+3=0\) i ma tylko jedno rozwiązanie. Pozostaje wyznaczyć te wartości parametru \(m\), dla których warunki zadania są spełnione, a równanie (2) jest kwadratowe, tj. wyznaczyć te wartości parametru, dla których spełnione są jednocześnie następujące warunki: \[ \begin{aligned} & \text { (W1) } m-2 \neq 0 \\ & \text { (W2) } \Delta>0 \\ & \text { (W3) } x_1 \cdot x_2>0 \\ & \text { (W4) } x_1+x_2>0 \\ & \text { (W5) }(m-2) \cdot 6^2-4 \cdot(m+3) \cdot 6+m+1 \neq 0 \end{aligned} \] Rozwiązaniem warunku (W1) jest \(m \neq 2\). Rozwiązujemy nierówność \(\Delta>0\) : \[ \begin{gathered} {[-4(m+3)]^2-4 \cdot(m-2) \cdot(m+1)>0} \\ 16 m^2+96 m+144-4 m^2+4 m+8=0 \\ 12 m^2+100 m+152>0 \\ m \in\left(-\infty,-\frac{19}{3}\right) \cup(-2,+\infty) \end{gathered} \] Korzystając ze wzorów Viète'a, rozwiązujemy warunek (W3): \[ \begin{gathered} x_1 \cdot x_2>0 \\ \frac{m+1}{m-2}>0 \\ (m+1)(m-2)>0 \wedge m \neq 2 \\ m \in(-\infty,-1) \cup(2,+\infty) \end{gathered} \] Korzystając ze wzorów Viète'a, rozwiązujemy warunek (W4): \[ \begin{gathered} x_1+x_2>0 \\ -\frac{-4(m+3)}{m-2}>0 \\ (m+3)(m-2)>0 \wedge m \neq 2 \\ m \in(-\infty,-3) \cup(2,+\infty) \end{gathered} \] Rozwiązujemy warunek (W5): \[ \begin{gathered} (m-2) \cdot 6^2-4 \cdot(m+3) \cdot 6+m+1 \neq 0 \\ 13 m-143 \neq 0 \\ m \neq 11 \end{gathered} \] Wyznaczamy część wspólną rozwiązań warunków (W1)-(W5) i otrzymujemy \(m \in\left(-\infty,-\frac{19}{3}\right) \cup(2,11) \cup(11,+\infty)\)
Udowodnij, że suma sześcianów trzech kolejnych liczb całkowitych niepodzielnych przez \(4\) jest liczbą podzielną przez \(36\).
Rozwiązanie CKE:
Sumę sześcianów trzech kolejnych liczb całkowitych niepodzielnych przez \(4\) można zapisać w postaci \[(a-1)^3+a^3+(a+1)^3\] gdzie \(a\) jest liczbą parzystą niepodzielną przez \(4\).
Ponieważ \[ (a-1)^3+a^3+(a+1)^3=a^3-3 a^2+3 a-1+a^3+a^3+3 a^2+3 a+1=3 a\left(a^2+2\right), \] więc liczba \((a-1)^3+a^3+(a+1)^3\) jest podzielna przez \(4\) jako iloczyn liczby parzystej \(3a\) i liczby parzystej \(a^2+2\).
Jeżeli \(a=3 k\), przy pewnym \(k \in \mathbb{Z}\), to \(3 a\left(a^2+2\right)=9 k\left(9 k^2+2\right)\) jest liczbą podzielną przez \(9\).
Jeżeli \(a=3 k+1\), przy pewnym \(k \in \mathbb{Z}\), to \[3 a\left(a^2+2\right)=3(3 k+1)\left[(3 k+1)^2+2\right]=\] \[=3(3 k+1)\left(9 k^2+6 k+3\right)=9(3 k+1)\left(3 k^2+2 k+1\right)\] jest liczbą podzielną przez \(9\).
Jeżeli \(a=3 k+2\), przy pewnym \(k \in \mathbb{Z}\), to liczba \[3 a\left(a^2+2\right)=\] \[ =3(3 k+2)\left[(3 k+2)^2+2\right]=3(3 k+2)\left(9 k^2+12 k+6\right)=9(3 k+2)\left(3 k^2+4 k+2\right) \] jest liczbą podzielną przez \(9\).
Zatem suma sześcianów trzech kolejnych liczb całkowitych niepodzielnych przez \(4\) jest podzielna przez \(9\). Ponieważ suma trzech kolejnych liczb całkowitych niepodzielnych przez \(4\) jest liczbą podzielną przez \(4\) i przez \(9\) oraz liczby \(4\) i \(9\) są względnie pierwsze, więc ta suma jest liczbą podzielną przez \(36\).
Na obrzeżach miasta znajduje się jezioro, na którym postanowiono stworzyć tor regatowy. Na podstawie dostępnych map wymodelowano w pewnej skali kształt linii brzegowej jeziora w kartezjańskim układzie współrzędnych \((x, y)\) za pomocą fragmentów wykresów funkcji \(f\) oraz \(g\) (zobacz rysunek). Funkcje \(f\) oraz \(g\) są określone wzorami \(f(x) = x^2\) oraz \(g(x)=-\frac{1}{2}\left(x-\frac{1}{2}\right)^2+4\). Początek toru postanowiono zlokalizować na brzegu jeziora w miejscu, któremu odpowiada w układzie współrzędnych punkt \(P = (-1, 1)\).
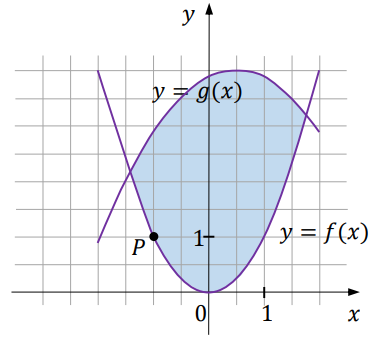
Niech \(R\) będzie punktem leżącym na wykresie funkcji \(g\).
Wykaż, że odległość punktu \(R\) od punktu \(P\) wyraża się wzorem \[|PR|=\sqrt{\frac{1}{4}x^4-\frac{1}{2}x^3-\frac{13}{8}x^2+\frac{39}{8}x+\frac{593}{64}}\] gdzie \(x\) jest pierwszą współrzędną punktu \(R\).
Rozwiązanie CKE:

Koniec toru regatowego należy umieścić na linii brzegowej.
Oblicz współrzędne punktu \(K\), w którym należy zlokalizować koniec toru, aby długość toru (tj. odległość końca \(K\) toru od początku \(P\)) była możliwie największa. Oblicz długość najdłuższego toru.
Zapisz obliczenia.
Wskazówka.
Przy rozwiązywaniu zadania możesz skorzystać z tego, że odległość dowolnego punktu \(R\) leżącego na wykresie funkcji \(g\) od punktu \(P\) wyraża się wzorem \[|PR|=\sqrt{\frac{1}{4}x^4-\frac{1}{2}x^3-\frac{13}{8}x^2+\frac{39}{8}x+\frac{593}{64}}\] gdzie \(x\) jest pierwszą współrzędną punktu \(R\).
\(K=\left(\frac{3}{2}, \frac{7}{2}\right)\), \(|PK|=\frac{5\sqrt{2}}{2}\)
Rozwiązanie CKE:

Rozwiąż równanie \[\sin (3x)=2\sin x\] w zbiorze \([0,\pi ]\).
\(x=0\), \(x=\frac{1}{6}\pi \), \(x=\frac{5}{6}\pi \), \(x=\pi\)
Rozwiązanie CKE:

Dany jest trapez równoramienny \(ABCD\) o obwodzie \(l\) i podstawach \(AB\) oraz \(CD\) takich, że \(|AB| \gt |CD|\). Trapez jest opisany na okręgu i wpisany w okrąg, a przekątna \(AC\) trapezu ma długość \(d\) (zobacz rysunek).
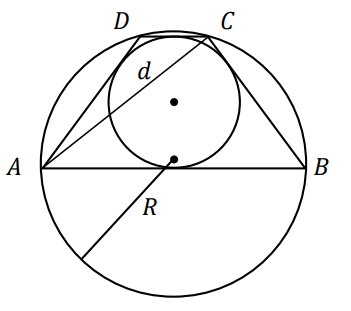
Wykaż, że promień \(R\) okręgu opisanego na trapezie \(ABCD\) jest równy \(\frac{d\cdot l}{2\sqrt{16d^2-l^2}}\)
Rozwiązanie CKE:

W kartezjańskim układzie współrzędnych \((x, y)\) punkt \(A = (9, 12)\) jest wierzchołkiem trójkąta \(ABC\). Prosta \(k\) o równaniu \(y = \frac{1}{2}x\) zawiera dwusieczną kąta \(ABC\) tego trójkąta. Okrąg \(\mathcal{O}\) o równaniu \((x - 8)^2 + (y - 4)^2 = 16\) jest wpisany w ten trójkąt.
Oblicz współrzędne punktu styczności prostej przechodzącej przez wierzchołki \(B\) i \(C\) tego trójkąta z okręgiem \(\mathcal{O}\).
Zapisz obliczenia.
\(y=0\) i \((8,0)\)
Rozwiązanie CKE:

Dany jest ostrosłup prawidłowy czworokątny \(ABCDS\) o podstawie \(ABCD\) i polu powierzchni bocznej równym \(P\). Kąt między wysokościami sąsiednich ścian bocznych poprowadzonych z wierzchołka \(S\) ma miarę \(2\alpha\). Objętość tego ostrosłupa jest równa \(\sqrt{k\cdot P^3\cdot \sin \alpha \cdot \cos (2\alpha )}\), gdzie \(k\) jest stałym współczynnikiem liczbowym.
Oblicz współczynnik \(k\).
Zapisz obliczenia.
\(k=\frac{\sqrt{2}}{36}\)
Rozwiązanie CKE:

Egzamin składa się z \(15\) zadań zamkniętych. Do każdego zadania podano cztery odpowiedzi, z których tylko jedna okazuje się poprawna. Zdający zalicza egzamin, jeśli udzieli poprawnych odpowiedzi w co najmniej \(11\) zadaniach. Pewien student przystąpił nieprzygotowany do egzaminu i w każdym zadaniu wybierał losowo odpowiedź. Przyjmij, że w każdym zadaniu wybór każdej z odpowiedzi przez studenta jest równo prawdopodobny.
Oblicz prawdopodobieństwo zdarzenia, że ten student zaliczył egzamin.
Zapisz obliczenia.
\(p=\frac{123841}{4^{15}}\)
Rozwiązanie CKE:











