Trapez
Poziom podstawowy
Trapez jest czworokątem, który ma dwa boki równoległe. Na rysunku poniżej równoległe są boki \(a\) i \(b\). 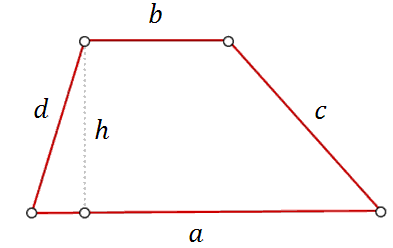
Pole trapezu obliczamy ze wzoru: \[P=\frac{1}{2}(a+b)\cdot h\]
W trapezie równoramiennym, który nie jest równoległobokiem, kąty przy ramieniu różnią się o \(50^\circ \). Kąt przy krótszej podstawie tego trapezu jest równy
A.\(115^\circ \)
B.\(120^\circ \)
C.\(125^\circ \)
D.\(130^\circ \)
W trapezie miary kątów ostrych są równe \(30^\circ \) i \(60^\circ \). Wówczas stosunek długości krótszego ramienia do dłuższego jest równy:
A.\( \frac{\sqrt{3}}{3} \)
B.\( \frac{1}{3} \)
C.\( \frac{\sqrt{2}}{2} \)
D.\( \frac{1}{2} \)
Rysunek przedstawia trapez prostokątny i długości trzech jego boków. 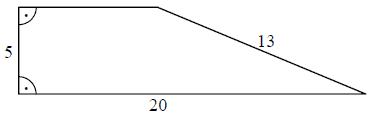 Obwód tego trapezu jest równy
Obwód tego trapezu jest równy
 Obwód tego trapezu jest równy
Obwód tego trapezu jest równy A.\( 43 \)
B.\( 46 \)
C.\( 48 \)
D.\( 50 \)
Różnica miar kątów wewnętrznych przy ramieniu trapezu równoramiennego, który nie jest równoległobokiem, jest równa \( 40^\circ \). Miara kąta przy krótszej podstawie jest równa.
A.\(120^\circ \)
B.\(110^\circ \)
C.\(80^\circ \)
D.\(70^\circ \)
Trapez jest prostokątny. Trójkąty podobne \(ABD\) i \(CBD\) są równoramienne. 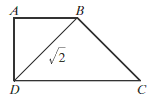 Obwód trapezu jest równy
Obwód trapezu jest równy
 Obwód trapezu jest równy
Obwód trapezu jest równy A.\( 4+2\sqrt{2} \)
B.\( 2\sqrt{2} \)
C.\( 4+\sqrt{2} \)
D.\( 4 \)
Podstawy trapezu prostokątnego mają długości \(6\) i \(10\) oraz tangens jego kąta ostrego jest równy \(3\). Oblicz pole tego trapezu.
W trapezie prostokątnym krótsza przekątna dzieli go na trójkąt prostokątny i trójkąt równoboczny. Dłuższa podstawa trapezu jest równa \(6\). Oblicz obwód tego trapezu.
Podstawy trapezu równoramiennego mają długości \(5\) i \(13\) oraz tangens kąta ostrego jest równy \(2\). Oblicz pole tego trapezu.
Podstawy trapezu prostokątnego mają długości \(6\) i \(10\) oraz tangens kąta ostrego jest równy \(3\). Oblicz pole tego trapezu.
Punkt \(E\) leży na ramieniu \(BC\) trapezu \(ABCD\), w którym \(AB\parallel CD\). Udowodnij, że \(|\sphericalangle AED|=|\sphericalangle BAE|+|\sphericalangle CDE|\).
Punkt \(E\) leży na ramieniu \(BC\) trapezu \(ABCD\), w którym \(AB\parallel CD\). Udowodnij, że jeżeli \(|EC|=|CD|\) oraz \(|EB|=|BA|\) to kąt \(AED\) jest prosty.
Trapez równoramienny \(ABCD\) o podstawach \(AB\) i \(CD\) jest opisany na okręgu o promieniu \(r\). Wykaż, że \(4r^2 = |AB| \cdot |CD|\).
W trapezie prostokątnym kąt ostry ma miarę \( 60^\circ \), a podstawy mają długość \(6\) i \(9\). Wysokość tego trapezu jest równa
A.\(6 \)
B.\(2\sqrt{3} \)
C.\(3\sqrt{3} \)
D.\(\frac{3\sqrt{3}}{2} \)
Wysokość trapezu równoramiennego o kącie ostrym \( 60^\circ \) i ramieniu długości \( 2\sqrt{3} \) jest równa
A.\(\sqrt{3} \)
B.\(3 \)
C.\(3\sqrt{3} \)
D.\(2 \)
W trapezie \( ABCD\ (AB || CD) \) przekątne \( AC \text{ i } BD \) przecinają się w punkcie \( O \) takim, że \( |AO|:|OC|=5:1 \). Pole trójkąta \( AOD \) jest równe \( 10 \). Uzasadnij, że pole trapezu \( ABCD \) jest równe \( 72 \). 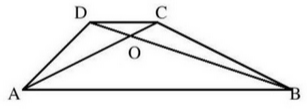

Tematy nadrzędne i sąsiednie